f値 統計の求め方と目安を具体例でわかりやすく解説

統計分析において、f値はデータ間のばらつきや差異を評価する重要な指標です。このf値は、統計学者ロナルド・A・フィッシャーが提唱した分散分析の一部として広く利用されています。

特に「f値とは 統計」における基本的な理解はもちろん、「f値 統計 求め方」や「f値 統計 大きい」といった具体的な評価基準が重要なポイントとなります。

また、「f値 統計 目安」を知ることは、分布表を使った実践的な判断に欠かせません。

本記事では、f値の基本から応用までを、f分布表を使った「f分布表 5%」などの具体例とともに解説します。これにより、f値を用いた分析がどのように意思決定や問題解決に役立つのかを明確にします。

注意事項）本記事でf値は統計におけるf値を指します。カメラでよく使うf：焦点距離、 F値（絞り値）ではないので注意してください。

f値 統計を完全攻略！基礎から応用まで

f値は、統計学においてデータ間の差異やばらつきを評価するための重要な指標です。この指標は分散分析の一部として、一元配置や多元配置での平均値の差が偶然か、それとも統計的に意味があるかを判断する際に使用されます。

その歴史は、1920年代に統計学者ロナルド・A・フィッシャーが分散分析を提唱したことに始まり、現在では幅広い分野で活用されています。

特にカメラ設計や画像処理においては、レンズの性能評価、製造プロセスの最適化、さらには異なる撮影条件やアルゴリズムの比較にf値が重要な役割を果たしています。

本記事では、f値の基礎、計算方法、分布表の使い方、さらにカメラ技術への具体的な応用例をわかりやすく解説します。

これにより、f値を活用したデータ分析がどのように製品開発や画像認識技術の向上に貢献するかを明らかにします。

f値とは？統計での重要な役割

f値は統計学において、データのばらつきや差異を評価する重要な指標です。一元配置分散分析や多元配置分散分析などで用いられ、特定の因子や条件間の平均値の差が偶然の範囲か、それとも意味のある差なのかを判断する際に活用されます。

例えば、カメラにおける画像解析では、異なる照明条件で撮影された画像の平均値や分散を比較し、環境条件が画像処理に与える影響を評価する際に使用されることがあります。

また、f値はp値を求める前段階で使用されることが多く、統計的有意性を検証する過程において欠かせない役割を果たしています。このため、統計学を活用する分野では、f値の計算と解釈が重要なスキルといえます。

f値の歴史

f値の概念は、統計学者ロナルド・A・フィッシャー（Ronald A. Fisher）が1920年代に提唱した「分散分析」（ANOVA: Analysis of Variance）から生まれました。フィッシャーはデータのばらつきを分析し、グループ間の違いを測定する方法として、f値を導入しました。
当時、農業実験などで異なる肥料や栽培方法が作物の成長に与える影響を調査する際に、この手法が用いられました。これが現在のf検定や分散分析の基礎となっています。

カメラ技術への応用においても、科学的な方法論を通じて、設計や評価プロセスの効率化が可能となり、f値はこれらの分野にもその重要性を広げてきました。

fの意味と由来

「f値」の「f」は、フィッシャー（Fisher）の頭文字から取られています。これにより、「f値」はフィッシャーによって導入された統計的な検定手法を指す用語として定着しました。

• 数学的背景: f値は、グループ間の分散とグループ内の分散の比率を表すもので、以下のように計算されます。 f=グループ間の分散グループ内の分散f = \frac{\text{グループ間の分散}}{\text{グループ内の分散}} この比率が大きいほど、グループ間の差異が統計的に有意である可能性が高まります。
• 統計的意義: f値は、仮説検定において、帰無仮説（差がないという仮定）を棄却するかどうかを判断するために使用されます。これにより、データの傾向やパターンを深く理解することができます。

カメラにおける歴史的視点

カメラ技術の進化に伴い、統計学の手法も利用されるようになりました。例えば、20世紀中頃には光学レンズの性能比較や製造プロセスの品質管理に分散分析が取り入れられ、f値が使用され始めました。また、デジタルカメラの普及とともに、画像認識や写真測量などの分野でも統計学が重要な役割を果たしています。

• 画像処理とf値（統計）: 例えば、異なる条件下で撮影した画像を比較する際に、統計的に有意な差異を評価するためにf値が用いられます。これにより、画像処理アルゴリズムやハードウェアの性能が客観的に評価可能となります。

f値は、ロナルド・フィッシャーによる分散分析から始まり、統計学全般にわたり広く使われる重要な指標です。その名前には、発案者であるフィッシャーへの敬意が込められています。

カメラの設計や評価の現場では、f値が画像の品質評価や製造工程の最適化、さらに新技術の開発において欠かせない役割を担っています。これにより、現代のカメラはますます高性能で使いやすい製品へと進化しています。

統計学におけるf値の使用場面

統計学のf値は、データ間のばらつきや差異を評価する際に広く使用されます。特にカメラの設計や工程において、以下のような具体的な場面で活用されています。

1. 異なるレンズ設計の性能評価

カメラの設計段階では、複数のレンズプロトタイプが作られます。それぞれのレンズで撮影した画像の解像度、色収差、コントラストを統計的に比較するためにf値が利用されます。

• 具体例: 異なる設計のレンズを用いて、同一条件下で撮影した画像のシャープネス（解像度）を測定します。一元配置分散分析を使用し、レンズ設計が画像性能に与える影響を評価します。この際、f値を計算することで、性能の違いが偶然ではなく実質的なものであるかを判断します。

2. 製造工程での品質管理

カメラの製造過程では、部品や工程間での品質差を確認するためにf値が使用されます。製品のばらつきを抑え、一定の基準を満たす品質を保証するために重要な指標となります。

• 具体例: 複数の製造ラインで生産されたイメージセンサーの感度データを分析します。感度のばらつきを統計的に評価し、製造ライン間に有意な差がある場合、f値を用いてその差を特定します。これにより、製造工程の改善点を明確にします。

3. 異なる撮影条件での画像性能評価

カメラがどのような条件下でも適切に機能するかを確認するため、異なる環境条件（照明、温度、湿度など）での性能評価にf値が活用されます。

• 具体例: 暗所、高照度、曇天などの異なる環境下で同一のカメラを使用して撮影した画像のノイズレベルを比較します。統計的な検証により、特定の条件でノイズレベルが大きく異なる場合、それが偶然でないかをf値を使って評価します。この結果を基に、カメラの設定やアルゴリズムを最適化します。

4. 画像処理アルゴリズムの比較

異なる画像処理アルゴリズム（例えば、ノイズ除去や色補正）の性能を比較する際にもf値が使用されます。

• 具体例: 異なるアルゴリズムを用いて処理された画像の色再現性やダイナミックレンジを評価します。f値を計算することで、どのアルゴリズムが他のものと比べて統計的に優れているかを判定できます。これにより、最適な画像処理技術を選択する判断材料となります。

5. 市場調査やユーザーテストでのフィードバック分析

カメラの開発段階で、ユーザーが異なるモデルや設定を使った際の満足度や評価スコアを比較するためにもf値が利用されます。

• 具体例: 3種類のカメラモデルについて、ユーザーが撮影した画像を基にした満足度スコアを比較します。一元配置分散分析でf値を用いてスコア間の差異を確認し、どのモデルが統計的に有意に高評価を得ているかを判断します。

---

f値は、カメラの設計から製造、性能評価、さらには市場調査に至るまで、統計的に信頼性のあるデータ分析を行うための鍵となる指標です。

これにより、データに基づいた設計や改善が可能となり、より優れた製品の開発が実現します。

f値 統計の求め方をわかりやすく解説

f値の計算は、分散分析を行う際の重要なステップです。具体的には、次のように計算されます

f値の基本的な計算式

f値は、以下の公式で計算されます：$$f = \frac{\text{因子間の分散（平均平方）}}{\text{誤差分散（平均平方）}}$$

• 因子間の分散: 異なるグループ間のばらつき。
• 誤差分散: グループ内の個々のデータのばらつき。

これにより、グループ間の差が偶然によるものか、統計的に意味のあるものかを判断できます。

因子間の分散とは？

「因子間の分散」とは、異なるグループ同士の平均値がどれくらい離れているかを示します。イメージしやすい例を挙げると：

• 異なる種類のカメラレンズ（レンズA, レンズB, レンズC）で撮影した画像の明るさを比較する場合
• 各レンズで得られた画像の明るさの平均値が大きく違えば、「因子間の分散」が大きいです。
• 逆に、各レンズの平均値がほぼ同じであれば、「因子間の分散」は小さくなります。

つまり、「因子間の分散」はグループ全体の違いを表す指標です。

誤差分散とは？

「誤差分散」とは、各グループ内でのデータのばらつきを示します。たとえば、レンズAだけを考えると：

• 同じレンズAを使って撮影した画像でも、明るさは完全に同じではなく少しずつ違います（環境や条件が影響するため）。
• この「同じグループ内の個々のデータの違い」を測るのが「誤差分散」です。

簡単に言えば、「誤差分散」は、同じグループ内でのデータの揺れ具合を表します。

比喩を使った解説

因子間の分散は、学校のクラスごとの平均テスト点数がどれくらい違うかを見るイメージです。例えば、クラスAの平均点が80点、クラスBの平均点が60点、クラスCの平均点が90点なら、因子間の分散は大きいです。

誤差分散は、クラス内での生徒ごとの点数のバラつきを見るイメージです。クラスAで、ほとんどの生徒が80点付近であれば誤差分散は小さいです。でも、生徒ごとに点数が50点から100点と大きくバラバラなら、誤差分散は大きくなります。

f値の計算手順

以下はf値を求める具体的な手順です。

1. 平方和（Sum of Squares, SS）の計算
   • 因子間平方和（SSB）: グループごとの平均と全体平均との差を2乗し、それに各グループのデータ数を掛けて合計します。
   • 誤差平方和（SSE）: 各データとその属するグループ平均との差を2乗して合計します。
   • 総平方和（SST）: 全データと全体平均との差を2乗して合計します。（※ SST = SSB + SSE）
2. 自由度（Degrees of Freedom, DF）の計算
   • 因子間の自由度: グループ数 – 1
   • 誤差の自由度: 全データ数 – グループ数
3. 平均平方（Mean Square, MS）の計算
   • 因子間の平均平方（MSB）: MSB=SSB因子間の自由度、$$MSB = \frac{SSB}{\text{因子間の自由度}}$$
   • 誤差の平均平方（MSE）: MSE=SSE誤差の自由度、$$MSE = \frac{SSE}{\text{誤差の自由度}}$$
4. f値の計算 $$f = \frac{MSB}{MSE}$$

カメラ設計を例とした具体的な計算例

シナリオ: 異なるレンズ設定（設定A, 設定B, 設定C）で撮影したカメラ画像の明るさ（輝度値）の平均に差があるか検証します。

• データ（カメラ輝度値）:
  • 設定A: 45, 50, 55
  • 設定B: 60, 65, 70
  • 設定C: 75, 80, 85

---

1. 平方和を求める
   • 全体平均: $$\text{全体平均} = \frac{45 + 50 + 55 + 60 + 65 + 70 + 75 + 80 + 85}{9} = 65$$
   • 各グループ平均:
     • 設定A: $$\text{平均A} = \frac{45 + 50 + 55}{3} = 50$$
     • 設定B: $$\text{平均B} = \frac{60 + 65 + 70}{3} = 65$$
     • 設定C: $$\text{平均C} = \frac{75 + 80 + 85}{3} = 80$$
   • 因子間平方和（SSB）:$$SSB = 3 \times (50 – 65)^2 + 3 \times (65 – 65)^2 + 3 \times (80 – 65)^2$$ $$ =3×225+3×0+3×225=1350$$
   • 誤差平方和（SSE）: $$SSE = (45 – 50)^2 + (50 – 50)^2 + (55 – 50)^2 + (60 – 65)^2 + \dots + (85 – 80)^2$$ $$SSE=25+0+25+25+0+25+25+0+25=150$$
   • 総平方和（SST）: $$SST=SSB+SSE=1350+150=1500$$

---

2. 自由度を計算する
   • 因子間の自由度: $$\text{グループ数} – 1 = 3 – 1 = 2$$
   • 誤差の自由度: $$\text{全データ数} – \text{グループ数} = 9 – 3 = 6$$

---

3. 平均平方を求める
   • 因子間の平均平方（MSB）: $$MSB = \frac{SSB}{\text{因子間の自由度}} = \frac{1350}{2} = 675$$
   • 誤差の平均平方（MSE）: $$MSE = \frac{SSE}{\text{誤差の自由度}} = \frac{150}{6} = 25$$

---

4. f値を計算する $$f = \frac{MSB}{MSE} = \frac{675}{25} = 27$$

計算されたf値（27）は、f分布表やp値を用いて統計的有意性を判断します。

例えば、有意水準5%（p < 0.05）の場合、f分布表での臨界値（自由度: 2, 6）は約5.14です。27はこれを超えるため、設定A, B, C間の明るさの差は統計的に有意と結論付けられます。

各計算の意味の解説

平方和（Sum of Squares, SS）の計算

平方和とは、データがどれだけバラついているかを数値化する指標です。データと基準（平均値など）の差を2乗して合計することで、ばらつきが大きいほど平方和も大きくなります。

• 因子間平方和（SSB）：因子間平方和は、グループ間の違いを測る指標です。
  • 各グループの平均値と全体平均値との差を2乗します。
  • その差にグループ内のデータ数を掛け、すべてのグループで合計します。
    意味: グループごとの違いが大きいほど、SSBも大きくなります。
• 誤差平方和（SSE）：誤差平方和は、グループ内でのデータのバラつきを測る指標です。
  • 各データと、その属するグループの平均との差を2乗して合計します。
    意味: グループ内でのデータの揺れ具合が大きいほど、SSEが増えます。
• 総平方和（SST）：総平方和は、すべてのデータのばらつきを全体平均値との違いとして計算したものです。
  • 因子間平方和（SSB）と誤差平方和（SSE）の合計で表されます。
    意味: 全体のデータがどれだけバラついているかの総量を示します。

自由度（Degrees of Freedom, DF）とは？

自由度とは、「計算に使える独立したデータの数」を指します。言い換えると、データを自由に変えられる範囲のことです。統計学では、自由度が多いほど、分析結果がより信頼性の高いものになります。

例えば、4つの数値があり、その合計が「10」であるとき、最初の3つの数値は自由に選べますが、4つ目の数値は「合計が10」という制約によって決まります。

このように制約がある場合、自由に変えられるのは「3つ」だけなので、自由度は「3」となります。

因子間の自由度（グループ数 – 1）

• 計算方法: 自由度は「グループ数 – 1」で計算されます。例えば、3つのグループがある場合、自由度は 3−1=2 です。
• 意味：グループ間の違いを測るために利用できる情報の数です。グループが増えると、比較できる情報も増えるため、自由度が大きくなります。自由度が少ないと、グループ間の差を正確に測るのが難しくなる場合があります。
• 例:カメラで3種類のレンズ（標準、望遠、広角）を比較する場合、レンズ間の違いを測るための自由度は 「3−1=2」 です。この2つの自由度を使って、どのレンズの違いが意味があるかを統計的に評価します。

誤差の自由度（全データ数 – グループ数）

• 計算方法: 自由度は「全データ数 – グループ数」で計算されます。
  例えば、15枚の写真があり、それが3つのグループ（各レンズごとに5枚ずつ）に分かれている場合、誤差の自由度は15−3=12 です。
• 意味:グループ内のデータ（写真）の揺れ具合を測る際に使える情報量を示します。自由度が多いほど、誤差の測定が正確になります。
• 例:あるレンズで5枚の写真を撮影したとします。それぞれの写真の明るさの違いを評価する際、全体で「5つ」のデータを持っていますが、「レンズ」という1つの制約があるため、自由に変えられるのは「5−1=4」 です。これがそのグループ内の誤差の自由度になります。

平均平方（Mean Square, MS）の計算

平均平方は、平方和を自由度で割った値で、「ばらつきの平均的な大きさ」を示します。

• 因子間の平均平方（MSB）：$$MSB = \frac{SSB}{\text{因子間の自由度}}$$
  意味: グループ間のばらつきが1つの自由度あたりどれくらいかを示します。これが大きいと、グループ間に明確な差がある可能性が高いです。
• 誤差の平均平方（MSE）：$$MSE = \frac{SSE}{\text{誤差の自由度}}$$
  意味: グループ内のデータのバラつきが、自由度1つあたりどれくらいかを示します。

f値の計算

$$f = \frac{MSB}{MSE}$$
意味: グループ間のばらつき（MSB）が、グループ内のばらつき（MSE）と比較してどれくらい大きいかを示します。f値が大きいほど、グループ間の違いが統計的に有意である可能性が高いです。

カメラ設計を例にした具体的なイメージ

カメラ設計で、異なるレンズタイプ（例: 標準レンズ、望遠レンズ、広角レンズ）で撮影した画像の明るさを比較する場合：

1. SSB（因子間平方和）：各レンズタイプの明るさ平均と全体の平均の差を計算します。これが、レンズごとの特性の違いを示します。
2. SSE（誤差平方和）：同じレンズで撮影した複数の画像の明るさのばらつきを計算します。これが、撮影条件（照明、環境など）による揺れを表します。
3. SST（総平方和）：すべての画像データについての明るさのばらつきを計算します。これは全体のデータの揺れ具合を示します。
4. f値の計算：f値を求めることで、異なるレンズ設定による明るさの違いが、単なる偶然か、それとも意味のある差かを判断できます。

f値（統計）が大きいときの統計的な意味とは

f値が大きいとはどういうことか？：値が大きい場合、因子間の分散（比較するグループの違い）が誤差分散（グループ内のデータのばらつき）よりも大きいことを示します。

これは、統計的に見てグループ間の差が偶然によるものではなく、意味のある差である可能性を高めます。

カメラ設計での具体例：異なる撮影条件での影響評価

●例1: 照明条件の影響を評価：カメラの性能を評価するために、以下の3つの撮影条件で同じ被写体を撮影するとします。

1. 昼間の自然光
2. 曇りの日の光
3. 夜間の人工照明

各条件で撮影した10枚の画像について、「画像の鮮明度」を数値化（例えば、コントラストやシャープネスのスコア）し、グループごとの平均とばらつきを比較します。

• 結果1: f値が大きい場合：f値が大きければ、昼間、曇り、夜間という条件が画像鮮明度に大きな影響を与えているといえます。これは、条件を考慮したカメラ設計（例えば、夜間撮影用の補正アルゴリズムや曇天時の自動調整機能）が必要であることを示唆します。
• 結果2: f値が小さい場合：f値が小さい場合は、照明条件による影響があまり見られないため、特定の条件に最適化する設計の必要性が低いことを示します。

●例2: レンズ種類の比較：異なるレンズ（標準、望遠、広角）で同じ被写体を撮影し、撮影画像の色収差（色のにじみ具合）を測定したとします。

• 結果1: f値が大きい場合：f値が大きければ、レンズの種類による色収差の差が統計的に有意であることを意味します。つまり、どのレンズを選ぶかが画像品質に大きく影響する可能性があるため、それに応じた選択や改善が求められます。
• 結果2: f値が小さい場合：f値が小さい場合、レンズ間の色収差の違いがあまりないことを示します。これは、レンズ間の設計が均等に優れている、または特定の条件下では違いが顕著ではないことを意味します。

f値が示す設計への重要性

• 大きなf値が示すもの：f値が大きい結果は、設計における改善の方向性を示します。例えば、特定の条件やレンズで問題が顕著であれば、その点を重点的に改良する必要があります。
• f値が小さい場合：小さいf値は、データがほぼ均一であることを示し、設計において条件や要素が安定していることを意味します。これにより、他の要因（例えば、センサーの精度や画像処理アルゴリズム）に焦点を当てる余地が生まれます。

---

カメラの設計においてf値を活用することで、特定の要因（照明条件やレンズの種類など）が画像品質に与える影響を明確に評価できます。

f値が大きければ、どの因子が有意な差をもたらすのかを把握し、改良の優先順位をつけることが可能です。これにより、より高品質なカメラの開発に役立つ分析が行えるのです。

f値の目安と基準：初心者向け解説

有意水準と基準値

統計分析では、通常は有意水準5%（0.05）が基準とされます。この水準は、「5%以下の確率で偶然起こる差」を意味し、これを超えた差があれば統計的に有意とみなします。

1. 有意差ありの判断基準
   • f分布表を参照して得られる基準値を「閾値」とします。
   • 計算されたf値が閾値を超えた場合、「有意差あり」と判断します。
2. 目安の具体例
   • 例えば、自由度（因子間: 4, 誤差: 20）の場合、有意水準5%での閾値は2.87です。
   • 計算したf値が3.2であれば、閾値（2.87）を超えているため、統計的に有意な差があると結論づけます。

有意水準5%を活用

後述するf分布表は、f値の基準値を提供するツールで、自由度と有意水準に応じた閾値を示しています。

（具体例での説明）

• 自由度（因子間: 5, 誤差: 15）の場合、有意水準5%での閾値は3.05。
• 計算したf値が3.5であれば、この閾値を上回っているため、差が有意であると判断します。

カメラ設計での応用例

ISO設定によるノイズ量の評価

カメラの異なるISO設定（100、400、800、1600）で撮影した画像を比較する場合:

1. 各設定の画像ノイズ量を数値化し、f値を計算します。
2. f値が閾値を超えれば、ISO設定の違いがノイズ量に統計的に有意な影響を与えていることがわかります。
   • 例えば、f値が4.1で閾値が3.2であれば、ISO設定ごとの差異が偶然ではないと結論づけられます。

ホワイトバランス設定の影響

異なるホワイトバランス設定（オート、昼光、蛍光灯）で撮影した画像の色調を比較する際:

• f値を利用して、設定ごとの色調の変化が有意かどうかを確認。
• 例えば、f値が閾値を超えている場合、ホワイトバランス設定が画像の色調に大きな影響を与えていることを示します。

f値の重要性

なぜ基準値が重要か？f値を基準値と比較することで、データ間の違いが統計的に意義深いかどうかを判断できます。正確な判断は、設計や製品開発における改善点を明確にする助けとなります。

注意点：f値や基準値は、データの数や自由度によって変化するため、適切なf分布表を参照することが不可欠です。有意水準の選択（通常5%）は、分析の目的に応じて調整が可能です。

---

f値を統計的に解釈する際には、有意水準と自由度に基づく基準値を明確に把握することが重要です。カメラの設計や設定評価の場面では、ISO感度やホワイトバランスなど、画像の品質に影響を与える要素の比較に活用できます。具体的な計算と分布表の活用により、設計や分析の精度が向上します。

f分布表の使い方をマスターしよう

f分布表は、自由度と有意水準を基に基準値を調べるために使用します。これにより、計算したf値が有意かどうかを判断できます。

例えば、自由度(3, 15)で有意水準5%のf値を調べたい場合、f分布表の該当する行と列の交差点を確認します。この基準値と実際のf値を比較して、帰無仮説を棄却するかどうかを判断します。

画像認識では、異なる解像度で撮影した画像のシャープネス比較の統計的評価において、f分布表を使用して差の有意性を確認することができます。

F分布表（5% 有意水準）

以下は自由度 (df1, df2) に基づくF分布表の一部です。有意水準5%（α=0.05）を基に作成されています。

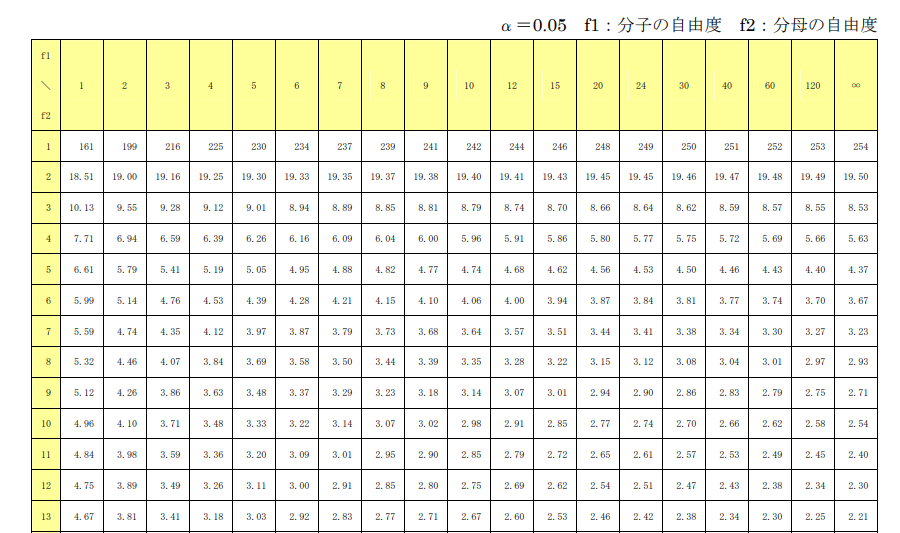
※参考URL：https://www.forming.co.jp/database/pdf/bunpu-F_005.pdf

F分布表の見方と使い方

F分布表は、自由度と有意水準に基づいてF値の基準値を調べるために使用します。この基準値を使って、計算したF値が統計的に有意かどうかを判定します。

分布表の構造

1. df2（誤差の自由度）列
   • 左側の最初の列（df2）は、データの「誤差の自由度」を表します。
   • 誤差の自由度は、全データ数からグループ数を引いた値です。
2. df1（因子の自由度）行
   • 上部の見出し部分（df1=1, df1=2など）は「因子の自由度」を表します。
   • 因子の自由度は、グループ数 – 1 で計算されます。
3. セルの値
   • 各セルには、有意水準に基づいたF値の基準値が記載されています。
   • 計算したF値がこの値を超えると「有意差がある」と判断されます。

分布表の読み方

1. 自由度を決める：自分のデータに基づき、以下の自由度を計算します:
   • 因子の自由度 (df1): グループ数 – 1
   • 誤差の自由度 (df2): 全データ数 – グループ数
2. 対応する基準値を探す
   • 分布表の左側から df2（誤差の自由度）を見つけます。
   • 上部から df1（因子の自由度）を見つけます。
   • 両者が交差するセルの値が、有意水準（例: 5%または1%）における基準値です。
3. F値と比較する：計算したF値と分布表の基準値を比較します:
   • F値 > 基準値 → 有意差あり
   • F値 ≤ 基準値 → 有意差なし

カメラの具体例での解説

例題：異なるISO設定（100, 400, 800）の3つのグループで、撮影した画像のノイズ量を比較します。以下のデータが得られました:

• データ数: 15（各グループ5枚ずつ）
• 因子の自由度 (df1): 3グループ – 1 = 2
• 誤差の自由度 (df2): 15データ – 3グループ = 12

F分布表の使い方

1. 自由度を確認
   • 因子の自由度 df1 = 2
   • 誤差の自由度 df2 = 12
2. 基準値を探す：5%有意水準の場合: 分布表で df1=2 と df2=12 の交差点を見る
   　　　　　　　→ 基準値は 3.89。
3. F値を比較：計算したF値が 4.2 だった場合:5%水準では 4.2 > 3.88 → 有意差あり。

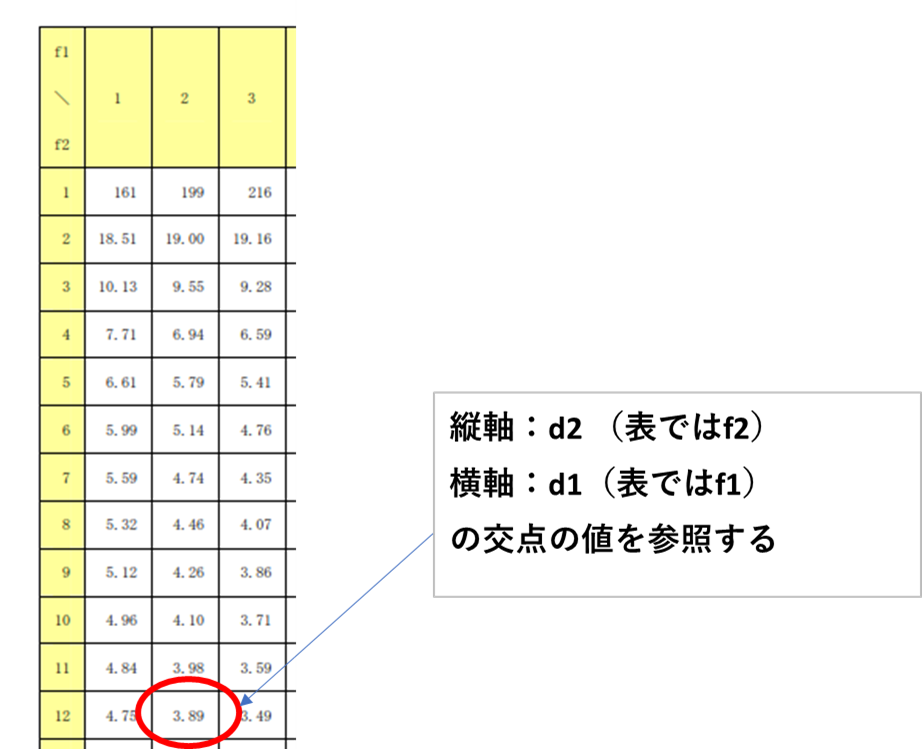
結論：ISO設定の違いが画像ノイズ量に影響を与えると考えられる。

---

この手順で、F分布表を使えば簡単にF値の有意性を判断できます。カメラの設定比較や画像解析の精度向上に活用してみましょう！

f値で有意かどうかを見極めるコツ

f値を用いた有意性の判定では、後述するp値の計算も重要です。f値を基にp値を求め、その値が有意水準（通常は0.05）以下であれば、有意な差があると判断します。

エクセルでは、F.DIST.RT関数を使うと簡単にp値を求められます。例えば、自由度(3, 16)で計算されたf値が4.5であれば、関数を用いて迅速に有意性を確認できます。

この手法は、複数のカメラモデル間の解像度性能を比較する場合にも役立ちます。

f値 統計の実践テクニックと応用事例

統計分析において、f検定とp値は、データ間の差異を科学的に評価するための強力なツールです。特に、f検定ではデータのばらつきを因子間と誤差間で分けて解析し、f値を基にp値を算出することで、データ間の差が偶然ではないと判断できます。

これらの指標は、科学研究や製品開発において重要な意思決定をサポートします。例えば、カメラ技術では、異なるISO設定やアルゴリズムの性能比較に利用され、最適な条件を導き出すための根拠を提供します。

本記事では、p値の基礎知識からf検定との関係、エクセルを使った計算手順、さらにはカメラの具体例を通じた実務での活用方法をわかりやすく解説します。これにより、統計分析を通じてデータに基づいた合理的な判断を可能にします。

f検定 p値の求め方とその活用方法

p値とは何か？

p値（確率値）は、統計的検定の結果を解釈するための重要な指標です。具体的には、帰無仮説（データ間に差がないという仮説）が正しいと仮定した場合に、現在のデータが観測される確率を示します。

• p値が小さい: 帰無仮説が成立する可能性が低い → データ間に有意な差があると判断。
• p値が大きい: 帰無仮説が成立する可能性が高い → データ間の差は偶然の範囲内と判断。

f値とp値の関係

f検定は、データ間の差を測るために使用され、計算の最終的な結果としてf値が得られます。このf値を基に、f分布表や統計ソフトを使ってp値を算出します。つまり、f値が大きいほどp値は小さくなり、データ間の差が有意である可能性が高まります。

f検定の流れとp値の求め方

1. f値の計算：因子間の分散を誤差分散で割ることで、f値を算出します。
   例: カメラのISO設定ごとのノイズ量を比較するとします。
2. 自由度の確認
   • df1: 因子の自由度（比較するグループの数 – 1）
   • df2: 誤差の自由度（データ全体の数 – グループ数）
3. f分布表または統計ソフトを使用：計算したf値と自由度を基に、f分布からp値を求めます。
   • エクセルの関数例: =FDIST(f値, df1, df2) でp値を計算。
   • 統計ソフトでは自動的にp値を出力します。
4. p値と有意水準の比較：一般的に、有意水準（例えば0.05）とp値を比較します。
   • p値 ≤ 0.05 → 有意差あり（帰無仮説を棄却）。
   • p値 > 0.05 → 有意差なし（帰無仮説を採択）。

p値の注意点

• p値の大小はサンプル数に依存: サンプル数が増えると、わずかな差でもp値が小さくなることがあります。
• 実務での解釈が重要: p値が小さくても、差が実務的に意味を持つかどうかを考慮する必要があります。
• カメラ設計での応用: 撮影モードやセンサー感度の調整による画質への影響を統計的に評価する際に、p値が役立ちます。

このように、p値を活用することで、カメラの設定や設計における統計的根拠を明確に示すことができます。

具体例: カメラのISO設定とノイズ評価

条件

• 目的: 異なるISO設定（100, 400, 800）によるノイズ量の差を検証。
• データ: 各設定で撮影した画像から得たノイズ値（単位: ノイズレベル）。
  • ISO 100: [10, 12, 11, 13]
  • ISO 400: [20, 22, 21, 23]
  • ISO 800: [30, 32, 31, 33]

1. f値の計算

1. 因子間平方和 (SSB)：グループの平均と全体平均との差を2乗して合計します。
   • 各グループの平均:
     • ISO 100 $$平均 = \frac{10 + 12 + 11 + 13}{4} = 11.5$$
     • ISO 400 $$平均 = \frac{20 + 22 + 21 + 23}{4} = 21.5$$
     • ISO 800 $$平均 = \frac{30 + 32 + 31 + 33}{4} = 31.5$$
   • 全体平均 = $$\frac{10 + 12 + 11 + 13 + 20 + 22 + 21 + 23 + 30 + 32 + 31 + 33}{12} = 21.5$$
   • SSB = $$4 \times [(11.5 – 21.5)^2 + (21.5 – 21.5)^2 + (31.5 – 21.5)^2]$$
     $$= 4 \times [(-10)^2 + 0^2 + 10^2] = 4 \times (100 + 0 + 100) = 800$$
2. 誤差平方和 (SSE)：各データとグループ平均との差を2乗して合計します。
   $$SSE = (10-11.5)^2 + (12-11.5)^2 + … + (33-31.5)^2$$
   $$= 2.25 + 0.25 + … + 2.25 = 30$$
3. 自由度 (DF)
   • 因子間の自由度: $$DF_1 = 3 – 1 = 2$$
   • 誤差の自由度: $$DF_2 = 12 – 3 = 9$$
4. 平均平方 (MS)
   • 因子間の平均平方: $$MSB = \frac{SSB}{DF_1} = \frac{800}{2} = 400$$
   • 誤差の平均平方: $$MSE = \frac{SSE}{DF_2} = \frac{30}{9} = 3.33$$
5. f値の計算
   $$f= \frac{MSB}{MSE} = \frac{400}{3.33} \approx 120.1$$

2. f値からp値を求める

• f値 = 120.1, 自由度 DF_1 = 2, DF_2 = 9。
• 分布表や統計ソフトでp値を確認します。有意水準5% (f分布表): 基準値 = 4.26

f値（120.1）は基準値も超えているため、p値は 0.01 未満です。つまり、有意差があると判断できます。

3. 解釈と活用

• 結論: 異なるISO設定によりノイズ量に有意な差が認められます。
• カメラの実務応用：この結果は、ISO感度を選択する際、ノイズの少ない条件（例えばISO 100）を優先するべきであることを示唆します。これにより、撮影モードの最適化やノイズリダクション機能の調整に役立てることができます。

---

注意点

• サンプルサイズの影響: データ数が少ないと結果が不安定になる場合があります。
• 実務的な差の確認: p値が小さくても、差が実際の運用で意味があるかを考えることが重要です。

このように、具体的な数値例とカメラの実務的な応用を組み合わせることで、f検定とp値の理解が深まります。

f検定 エクセルで手軽に統計分析する方法

エクセルを使用してf検定を行う手順を具体的に解説します。以下の手順を参考にして、実際に計算を行ってみましょう。

手順 1: データを入力

1. 比較したいグループごとのデータを列に入力します。例: カメラのISO設定ごとのノイズ量データ
   • 列 A (ISO 100): 10, 12, 11, 13
   • 列 B (ISO 400): 20, 22, 21, 23
   • 列 C (ISO 800): 30, 32, 31, 33

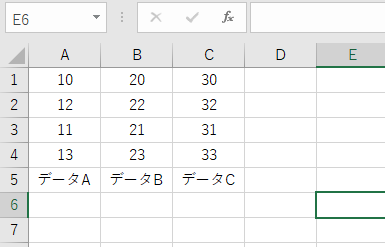
手順 2: 分散の等質性を確認

f検定は分散が等しいことを前提とします。エクセルで分散を確認する方法は次の通りです。

1. 空いているセルに分散関数 =VAR.S(範囲) を入力します。
   • ISO 100 の分散: =VAR.S(A1:A4)
   • ISO 400 の分散: =VAR.S(B1:B4)
   • ISO 800 の分散: =VAR.S(C1:C4)

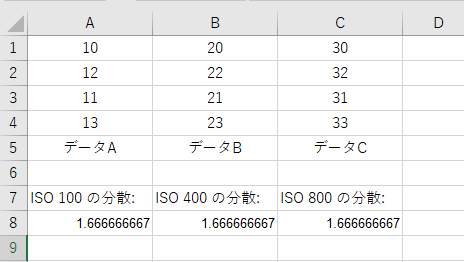
手順 3: f検定ツールを有効化

1. エクセル上部のリボンから [データ] タブを開きます。
2. [データ分析] をクリックします。（データ分析ツールが見つからない場合は以下を参照）
   • 有効化方法:
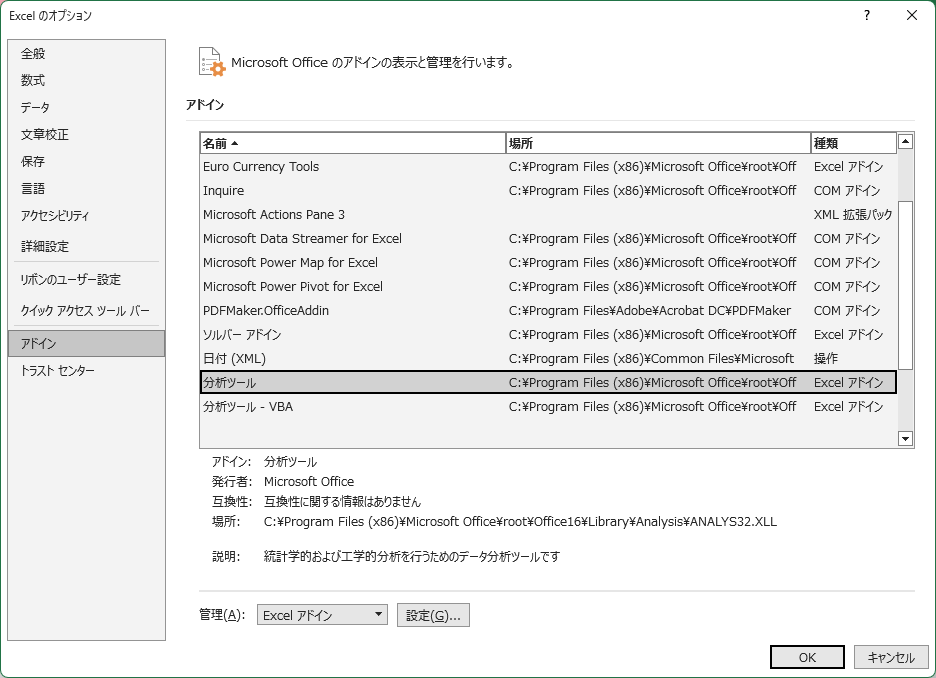
     • [ファイル] → [オプション] → [アドイン] → [Excelアドイン] を選択。
     • 分析ツール にチェックを入れて有効化します。

手順 4: f検定を実行

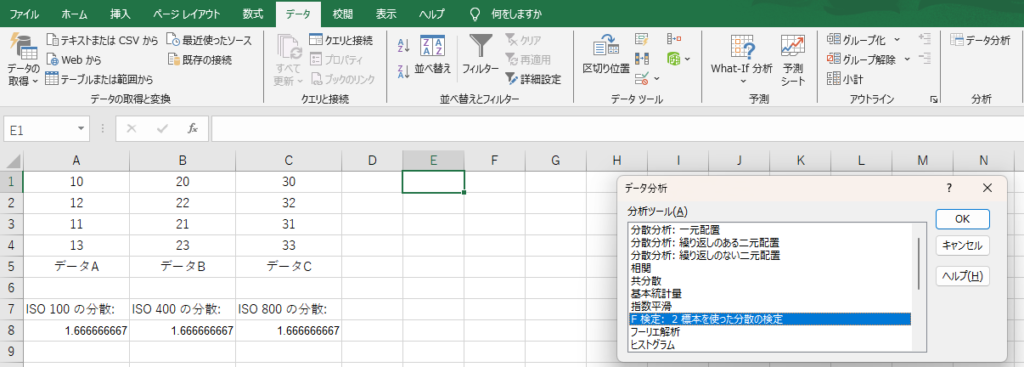
1. [データ分析] ウィンドウで f検定: 二標本による分散の検定 を選択。
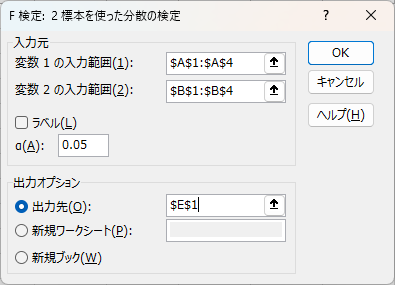
2. 入力範囲を指定:
   • グループ 1（例: ISO 100）→ 範囲 A1:A4
   • グループ 2（例: ISO 400）→ 範囲 B1:B4
3. 出力先を選択: 分析結果を表示するセルを指定（例: E1）。
4. OK をクリック。

手順 5: 結果の確認

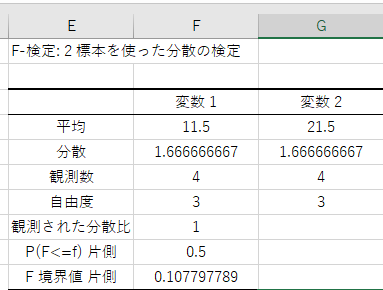
出力された結果には次のような情報が含まれます：

• f値 (F): 例では計算結果が0.1077。
• p値: 自由度に基づく有意性（例: p値が 0.001 以下なら有意）。
• 自由度 (df): 因子と誤差の自由度が表示されます。

手順 6: 複数グループを比較する場合

エクセルの標準機能では二つのグループ間でのf検定のみ実施可能です。複数グループを比較する際には、次の方法を検討してください：

1. ANOVA（分散分析） を使用: [データ分析] → [分散分析: 一元配置] を選択。
2. グループデータ範囲（例: A1:C4）を入力し、結果を確認します。

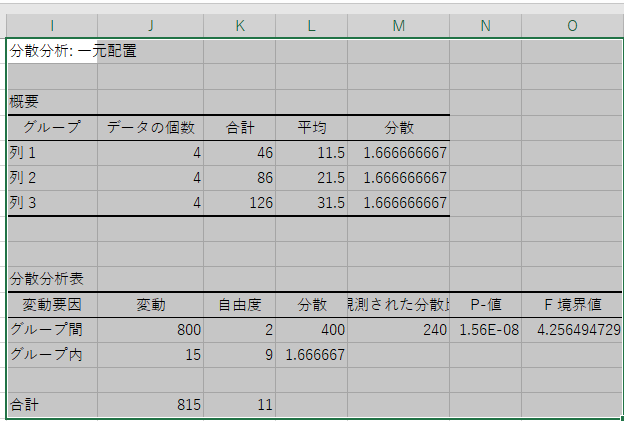
具体例: ISO設定のノイズ量比較

• グループデータ（ISO 100, 400, 800）を入力。
• 分散を比較すると、ISO 100 = 1.67, ISO 400 = 1.67, ISO 800 = 1.67。分散が等しいことを確認。
• f検定を実施し、ISO 100 と ISO 400 を比較:
  • f値: 0.1077
  • p値: 0.5

結果から、ノイズ量に有意差が無しと判断できます。

---

注意事項

• p値が非常に小さい場合、エクセルでは科学記数法（例: 1.2E-04）で表示されます。
• 分散が等しくない場合、等分散を仮定しない検定を別途使用する必要があります（例: Welch検定）。

エクセルを活用することで、複雑な統計計算を手軽に行い、カメラの設定間の差異を明確に評価できます。

写真測量でのf値活用

写真測量は、複数の画像を用いて地形や対象物の寸法を測定する技術です。この分野で f値（統計） を活用することで、撮影条件が測量精度にどのように影響するかを分析できます。以下に、初心者にも理解しやすい具体例を挙げて解説します。

実例: 異なる撮影条件による測量精度の比較

条件

測量対象の地形を撮影する際に、以下の3つの条件でカメラを設定したとします。

1. 高さ 10m
2. 高さ 20m
3. 高さ 30m

各条件で撮影した画像を解析して、対象の位置情報（例えば、対象物の緯度・経度座標）を計算。その後、各条件での位置情報のばらつきを比較し、どの高さでの撮影が最も正確かを判断します。

ステップ 1: データの収集

各高さで10枚ずつ画像を撮影し、座標データを得ます。

• 高さ 10m: 座標ばらつき（例: ±1.5m）
• 高さ 20m: 座標ばらつき（例: ±0.8m）
• 高さ 30m: 座標ばらつき（例: ±2.0m）

ステップ 2: f値の計算

1. 各高さのデータから分散を求めます。
   • 高さ 10m の分散: 2.25
   • 高さ 20m の分散: 0.64
   • 高さ 30m の分散: 4.00
2. 因子間の分散と誤差分散を計算します。
   • 因子間の分散: 異なる高さ条件間のばらつき。
   • 誤差分散: 同じ高さ内のデータばらつき。
3. f値を算出:
   • 例: $$f = \frac{\text{因子間の分散}}{\text{誤差分散}} = 5.4$$

ステップ 3: 分布表から有意性を確認

1. 自由度を確認します。
   • 因子間自由度 (df_1): 2（条件が3つの場合、3 – 1）
   • 誤差自由度 (df_2): 27（各条件で10データ、総データ数30 – 条件数3）
2. f分布表を用いて、5%有意水準で基準値を確認。
   • 5%有意水準の基準値（df_1 = 2, df_2 = 27）は 3.35。
3. 計算した f値（5.4）が基準値（3.35）を上回っているため、有意差ありと判断。

ステップ 4: 結果の解釈

f検定の結果、撮影高さが測量精度に有意な影響を与えることが示されました。具体的には、高さ 20m で撮影した画像が最も精度が高い（ばらつきが最小）という結論に至ります。

ステップ 5: 実務への応用

• 測量計画では、高さ 20m を基準とした撮影条件を設定する。
• 他のプロジェクトでも同様の分析を行い、最適な撮影条件を検討。

---

ポイント

• f値を活用することで、複数の条件を比較し、測量精度の高い条件を科学的に選定可能です。
• カメラの設定（高さ、角度、解像度）を統計的に最適化することで、プロジェクト全体の効率と正確性が向上します。

このように、写真測量におけるf値の活用は、初心者でも取り組みやすいデータ分析の一例となります。

f値を活かした画像認識の応用テクニック

画像認識において、f値（統計） は、異なるアルゴリズムやモデルを客観的に比較するために非常に有用です。ここでは、具体的な応用例を挙げて解説します。

実例 1: 画像認識モデルの性能比較

条件

2種類の画像認識モデル（従来型と最新型）の性能を比較します。

• 従来型モデル: 正確性（Accuracy）80%、誤認識率（False Positive Rate）20%
• 最新型モデル: 正確性85%、誤認識率15%

これらのモデルの違いが統計的に有意かどうかを検証します。

手順:

1. データ収集
   • 各モデルで、100枚の画像を分類させた結果を収集します。
   • 従来型: 正確な分類 80枚、誤分類 20枚。
   • 最新型: 正確な分類 85枚、誤分類 15枚。
2. f値の計算
   • 因子間の分散: モデル間の差異（正確な分類率や誤認識率の違い）
   • 誤差分散: 同じモデル内での結果のばらつき
   $$f = \frac{\text{因子間の分散}}{\text{誤差分散}} $$
   計算の結果、f値が4.2となりました。
3. 有意性の確認
   • 自由度 (df_1 = 1, df_2 = 198) を基にf分布表を参照します。
   • 5%有意水準の基準値が3.89であり、4.2 > 3.89 のため、有意差ありと判断。

結果の解釈:

最新型モデルの精度向上は統計的に有意であり、現場では最新型モデルを採用するべきと結論づけられます。

実例 2: ノイズ除去アルゴリズムの評価

条件

異なるノイズ除去アルゴリズム（アルゴリズムAとアルゴリズムB）の効果を比較します。

• アルゴリズムA: ノイズ除去率70%、処理時間0.5秒。
• アルゴリズムB: ノイズ除去率80%、処理時間0.6秒。

どちらがより効果的か、f検定を用いて検証します。

手順:

1. データ収集：50枚の画像を各アルゴリズムで処理し、ノイズ除去率を記録します。
2. f値の計算
   • 因子間の分散: アルゴリズムAとBのノイズ除去率の違い。
   • 誤差分散: 各アルゴリズム内での結果のばらつき。
   計算の結果、f値が5.6となりました。
3. 有意性の確認
   • 自由度 (df_1 = 1, df_2 = 98) を基にf分布表を参照。
   • 5%有意水準の基準値が4.08であり、5.6 > 4.08 のため、有意差ありと判断。

結果の解釈:

アルゴリズムBはノイズ除去性能で統計的に優れていることが確認されます。多少の処理時間増加は許容範囲とし、アルゴリズムBを選定します。

画像認識分野でのf値活用のメリット

1. 客観的な比較が可能: モデルやアルゴリズムの性能差を統計的に評価できるため、感覚に頼らずデータで判断できます。
2. 最適な選択ができる: 統計的有意性を基に、効率性や正確性の高い選択肢を選べます。
3. 開発プロセスの改善: 計測結果を元にさらなる改善案を導き出し、高精度な画像認識技術の実現につながります。

---

画像認識の精度向上において、f値の活用は信頼性の高い判断を可能にし、現場での効率的なアルゴリズム選定に役立ちます。

f値 統計の基礎から応用まで完全ガイドのまとめ

本記事のまとめを以下に列記します。

• f値は統計分析でデータ間のばらつきや差異を評価する指標
• 分散分析において、一元配置や多元配置で利用される
• f値は因子間の分散と誤差分散の比率を表す
• f値が大きいほどグループ間の差異が有意である可能性が高い
• f値は1920年代にフィッシャーが提唱した分散分析から生まれた
• カメラ設計ではレンズ性能や製造工程の評価に使われる
• 異なる撮影条件でのノイズや解像度の比較にも活用される
• 画像処理アルゴリズムの性能評価にも有用
• f値はp値を求める際の中間指標として利用される
• f分布表を参照し、計算したf値の有意性を判断する
• 自由度に基づいて適切なf分布表を選択する必要がある
• ISO設定やホワイトバランスの影響を統計的に検証できる
• エクセルを使えばf値やp値の計算が容易に行える
• 写真測量や画像認識などの具体例でf値の有効性が示される
• f値を活用することでカメラ製品の品質向上に寄与する