Cpk計算式を基礎から解説！工程能力指数の全知識

Cpk計算式は、製造現場で工程能力指数（Cpk）を正確に計算し、品質管理を効率化するための基本的なツールです。この記事では、Cpkとは何か、その計算方法、さらに両側規格に対応したCpk計算式や、エクセルを活用した具体的な手順を詳しく解説します。

また、CpkとPpkの違いや、CpとCpk計算式の比較、工程能力（K）の計算方法など、品質管理に必要な知識を網羅します。Cpk計算サイトの活用や標準偏差（σ値）の影響についても触れ、Cpkの正しい使い方を理解することで、現場の改善に役立ててください。

品質管理やエクセルを使った計算に興味がある方に向けて、初心者にも分かりやすい内容をお届けします。

記事のポイント

Cpk計算式の基礎と工程能力指数の重要性を理解できる
両側規格や片側規格におけるCpk計算方法を学べる
エクセルや計算サイトを活用したCpk計算の具体例を把握できる
Cp、Cpk、Ppkの違いや標準偏差（σ値）の影響を理解できる

Cpk計算式を完全攻略！基礎から学べるガイド
Cpk計算式で工程改善を最大化する方法

Cpk計算式を完全攻略！基礎から学べるガイド

Cpk（工程能力指数）は、製造工程の品質を数値で示す指標で、特にばらつきと偏りを評価するために利用されます。

その起源は20世紀前半に統計的品質管理（SQC）として提唱された手法にありますが、1980年代以降、製造業の競争力を高めるために広く活用されるようになりました。Cpkの活用によって、製造現場での品質基準が可視化され、改善の方向性が明確になります。

この記事では、Cpkの歴史や重要性、さらに品質管理の現場でどのように利用されているのかについて詳しく解説します。

Cpkとはその歴史と重要性：初心者にもわかりやすく解説

Cpk（工程能力指数）は、製造現場において製品品質を数値で表し、管理するための重要な指標です。その歴史や重要性、さらにはCpkから得られる情報を初心者にもわかりやすく解説します。

Cpkの誕生と使われ始めた経緯

Cpkは、20世紀後半に品質管理の手法として広がりました。その背景には、アメリカや日本を中心に、製造業での品質管理がますます重要視されるようになったことがあります。

起源:Cpkの基盤となる考え方は、1920年代にウォルター・シューハートが提唱した統計的品質管理（Statistical Quality Control, SQC）に由来します。シューハートのアイデアは、製造工程のばらつきを統計的に管理するというものでした。
広がり:特に1980年代、日本企業が「品質で勝つ」と世界的に注目される中、Cpkが国際的な品質管理手法として広まりました。例えば、トヨタ生産方式では、Cpkを活用して工程の安定性と効率化を実現しました。
今日の状況:現在では、ISO（国際標準化機構）や各国の品質規格にもCpkが含まれ、製造業の品質評価で欠かせない基準となっています。

Cpkの重要性とは？

Cpkが重要視される理由は、製品やプロセスの「信頼性」を数値で明確に示すことができるからです。これにより、次のようなメリットがあります。

品質基準の達成度を明確化：Cpkは、製造工程が規格範囲内で製品を作れているかを示します。たとえば、数値が高いほど「規格に適合した製品が多い」と分かります。
顧客満足度の向上：規格外の製品が少なければ、不良品が減り、顧客に高品質な製品を届けることができます。
コスト削減に貢献：安定した工程を維持することで、手直しや廃棄にかかるコストを削減できます。
問題の早期発見：Cpkの数値が低下した場合、工程に異常があることを示すため、早期に改善対応が可能です。

Cpkから分かること

Cpkを用いることで、製造工程に関する以下のような情報を得ることができます。

工程の安定性：規格範囲内に製品がどれだけ収まっているかを数値で把握できます。たとえば、Cpkが「1.33以上」であれば、多くの業界で「合格」とされます。
ばらつきの影響：製品寸法や特性値が規格の中心からどれだけ離れているか、また、そのばらつきがどの程度であるかがわかります。
不良品率の予測：Cpk値をもとに、工程がどれくらい不良品を出しているかを予測できます。これにより、工程の改善ポイントが明確になります。
片側規格や両側規格の対応：規格が片側だけか、両側に制限があるかを考慮し、柔軟に評価が可能です。

Cpkのイメージ

Cpkは、製造現場で工程を管理し、製品の品質を保証するための「健康診断のような指標」と言えます。健康診断で血圧や体温を測るのと同じように、Cpkを測定することで工程の「健康状態」を知ることができます。

たとえば、カメラ製造では、レンズの研磨工程やシャッター部品の寸法精度がわずかにズレただけで、全体の性能に大きな影響を与える可能性があります。このような精密な工程では、Cpkが非常に重要な役割を果たします。

Cpkを正しく理解し、使いこなすことで、製造現場での品質管理が効率的かつ確実になります。まずは、自分の業務にCpkを取り入れ、小さな改善を積み重ねるところから始めてみましょう。

CPとCpkの違いをわかりやすく解説

CP（工程能力）とCpk（工程能力指数）は、どちらも製造工程の能力を測るための指標ですが、評価する視点や特性が異なります。これらの違いを詳細に説明し、数値や具体的な特徴を交えて解説します。

CPとは？（工程能力）

CPは、工程のばらつきが仕様範囲内にどれだけ収まっているかを測る指標です。この指標は、工程の中心値が規格の中央からズレているかどうかを考慮しません。そのため、工程が規格から外れていても、ばらつきが小さい場合には高いCP値を示すことがあります。

計算式
$$CP = \frac{{USL – LSL}}{{6σ}}$$

USL（Upper Specification Limit）：上限値
LSL（Lower Specification Limit）：下限値
6σ：工程のばらつきを表す範囲（標準偏差σの6倍）

特徴

工程のばらつきを純粋に評価する指標。
中心値のズレ（偏り）を無視する。
数値が 1.33以上 であれば、一般的に「工程能力あり」とされる。

Cpkの計算式は？（工程能力指数）

Cpkは、CPの評価に「工程の偏り」を加味した指標です。製品特性が仕様範囲の中央に近いかどうかを考慮するため、現実的な品質評価が可能です。

計算式
$$Cpk = \min\left( \frac{{USL – \bar{X}}}{{3σ}}, \frac{{\bar{X} – LSL}}{{3σ}} \right)$$

Xˉ（平均値）：工程の中心値
上限（USL）と下限（LSL）からの距離をそれぞれ評価し、小さい方を採用。

特徴

工程の中心値が規格の中央からズレている場合、低い値になる。
数値が 1.33以上 であれば「安定した工程能力」とされる。
偏りを考慮するため、CPよりも厳密な評価が可能。

CPとCpkの数値例での比較

例えば、カメラのシャッター部品の加工工程を考えてみます。

規格範囲（USL – LSL）：50 ± 0.5mm
工程の標準偏差（σ）：0.05mm
平均値（average_X）が50.2mmにズレている場合

CPの計算 $$CP=（50.5−49.5）/ （６×0.05）=3.33$$

Cpkの計算
$$Cpk = \min\left( \frac{{50.5 – 50.2}}{{3 \times 0.05}}, \frac{{50.2 – 49.5}}{{3 \times 0.05}} \right)$$
$$Cpk = \min\left( \frac{{0.3}}{{0.15}}, \frac{{0.7}}{{0.15}} \right) = \min(2, 4.67) = 2$$

結果として、この場合、CPは高い工程能力を示しますが、Cpkでは中心値がズレていることが反映されます。

CPとCpkの比較表

指標	計算式	特徴	長所	短所
CP	(USL-LSL)/6σ	工程のばらつきを評価。中心値のズレは考慮しない。	簡単に計算可能	偏りを無視するため、実際の品質を反映しにくい
Cpk	Min(下限Cpk、上限Cpk）の低い方	偏りを含めて工程を評価。現実的な品質を示す。	偏りを考慮することで正確な評価が可能	計算がやや複雑

Cpkが重要な理由

製造現場では、実際の製品が規格範囲に収まるだけでなく、中心値に近いことも求められます。Cpkはその要件を満たしているかを評価するため、特にカメラ製造のような精密な工程で不可欠です。

例えば、センサーの感度調整やレンズの焦点精度など、わずかなズレが大きな影響を与える工程では、Cpkの評価が高い信頼性を持ちます。

CPとCpkを適切に使い分けることで、工程管理をより効果的に進められます。

CPとCpkの使い分けについて

CP（工程能力）とCpk（工程能力指数）は、評価の視点や目的によって使い分けることが重要です。それぞれの特性に基づいて、どのような場面で適切に利用すべきかを詳しく解説します。

CPは工程のばらつきを評価する指標で、偏りを無視するため、以下のような場面で有効です。

工程の設計段階
- 新しい工程を設計するときや改善を計画するときに、ばらつきを最小限に抑える能力を確認する場合に使用します。
- 例：カメラのレンズを研磨する工程で、仕上がりの厚みのばらつきが設計値の範囲内に収まるかを確認する。
規格中心が確実に合っている場合
- 工程がすでに規格の中央に合っていると確信できる状況では、偏りを考慮する必要がないため、CPで十分です。
初期診断や大まかな比較
- 複数の工程のばらつきの大きさを比較する際、CPを使うと簡単に傾向を把握できます。

Cpkは、ばらつきと中心値の偏りの両方を考慮するため、実際の工程能力を評価する場面で有効です。

運用中の工程の品質確認
- 製造現場で、完成品の品質を評価する際にはCpkが適しています。
- 例：カメラセンサーの感度が規格範囲内であるだけでなく、規格中央に近い値を保っているかを評価する。
偏りが発生しやすい工程
- 素材や加工条件によって、平均値が規格範囲の中央からズレやすい工程では、Cpkが重要です。
- 例：カメラのシャッター速度調整工程で、設定値がズレる可能性を含めて評価する。
顧客に品質を保証する場合
- 顧客に対して、製品が仕様どおりであることを説明する際には、Cpkが信頼性の高い指標となります。
製造トラブルの原因特定
- 不良品が発生した場合、その原因がばらつきによるものか、偏りによるものかを判断するためにCpkが役立ちます。

CPとCpkの使い分けのポイント

評価の目的	使うべき指標	理由
工程のばらつきを単純に評価する	CP	規格範囲に対するばらつきだけを確認するため。
工程が仕様範囲内にあるかどうかを確認する	Cpk	中心値の偏りも加味した現実的な評価が必要だから。
新しい工程の設計や初期診断	CP	中心値の調整を前提とした設計時には、ばらつきだけを評価すれば十分だから。
顧客に品質を保証する	Cpk	偏りを含めた品質評価が信頼性を高めるから。
不良の原因がばらつきか偏りかを特定する	Cpk	中心値の偏りが不良率に与える影響を評価するため。

実際の使い分け例

例えば、カメラの製造工程でレンズの厚みを管理する場合：

初期段階：工程が仕様に基づいてばらつきを抑えられるかを確認するため、CPを計算。
（例：CP = 1.5なら、十分にばらつきが小さい工程と判断）
量産段階：実際の厚みが規格範囲の中央に近いかどうかも確認するため、Cpkを計算。
（例：Cpk = 1.2なら、許容範囲内だが若干の偏りがある可能性を考慮）

CPとCpkは、目的によって使い分けることで、より的確に工程の状況を把握し、品質向上を実現できます。工程のばらつきや偏りの原因を見極め、適切な指標を用いることが、安定した製品品質を保つ鍵となります。

工程能力指数の計算方法とは

以下に、30個のサンプルデータを使ってCpkを算出する計算過程を順序よく説明します。

1. サンプルデータの収集

まず、30個のデータを測定します。以下は仮のデータ例です。Cpkを算出するにはある程度のサンプルデータが必要であり、最低でも30個サンプルデータは用意しましょう。

1.2, 1.5, 2.1, 1.8, 0.9, 2.3, 1.4, 1.9, 1.7, 2.0,
1.3, 1.6, 2.2, 0.8, 2.1, 1.5, 1.1, 1.8, 2.0, 1.9,
1.7, 1.3, 2.4, 1.4, 1.6, 1.5, 1.8, 1.2, 1.9, 1.5

2. 平均値 (μ) を計算

データの平均値を求めます。 μ=データの合計データの個数$$\mu = \frac{\text{データの合計}}{\text{データの個数}}$$

例: $$μ= \frac{1.2 + 1.5 + 2.1 + \ldots + 1.5}{30} = 1.62$$

3. 標準偏差 (σ) を計算

次に、標準偏差を計算します。

標準偏差の公式: $$\sigma = \sqrt{\frac{\sum (x_i – \mu)^2}{n}}$$

xi: 各データ
μ: 平均値
n: データ数

計算例:

各データ点の偏差を（各データ – 平均値）で計算
例 （1.2 – 1.62）、（1.5 – 1.62）、（2.1 – 1.62）・・・
偏差の二乗を合計。（※２乗することで、負の値も正の値になる。）
例 （1.2 – 1.62)² + (1.5 – 1.62)² + ( 2.1 -1.62)² ・・・
データ数 n=30 で割る。
例 ｛（1.2 – 1.62)² + (1.5 – 1.62)² + ( 2.1 -1.62)² ・・・｝ / 30
平方根を取る。（※上記で２乗したので、元に戻すため）
例 √[｛（1.2 – 1.62)² + (1.5 – 1.62)² + ( 2.1 -1.62)² ・・・｝ / 30 ]

結果: $$\sigma = 1.80 $$

4. Cpkの計算式を確認

Cpkの公式は以下の通りです：$$ Cpk = \min \left( \frac{\text{USL} – \mu}{3\sigma}, \frac{\mu – \text{LSL}}{3\sigma} \right)$$

USL（上限規格値）: 10
LSL（下限規格値）: -10
μ（平均値）: 1.62
σ（標準偏差）: 1.80

5. 上限側と下限側の能力指数を計算

上限側の能力指数

$$\frac{\text{USL} – \mu}{3\sigma} = \frac{10 – 1.62}{3 \times 1.80} = \frac{8.38}{5.40} = 1.55$$

下限側の能力指数

$$\frac{\mu – \text{LSL}}{3\sigma} = \frac{1.62 – (-10)}{3 \times 1.80} = \frac{11.62}{5.40} = 2.15$$

6. 最小値を選択

Cpkは上限側と下限側の値のうち小さい方を採用します。$$ Cpk=min⁡(1.55,2.15)= 1.55$$

7. 結果の解釈

Cpk値が 1.55 であることから、この工程は非常に高い能力を持ち、製品が規格内に収まる確率が高いことが分かります。

Cpk ≥ 1.33: 工程は安定的で高い能力を持つ。
Cpk < 1.33: 改善が必要。

サンプルデータを使ったCpk計算の要点

サンプルデータを30個以上収集。
平均値と標準偏差を計算。
Cpkの公式に代入して結果を求める。
Cpk値の大小により工程の品質を評価。

これにより、工程のばらつきを数値化し、改善ポイントを特定できます。

製造現場でCpk管理するメリット

製造現場でCpk管理を行うことには、多くのメリットがあります。特に、カメラ製造のように高い精度が求められる現場では、以下のような効果が期待できます。

1. 製品品質の安定化

Cpk管理を導入することで、製造工程が規格範囲内で安定しているかどうかを定量的に把握できます。これにより、不良品の発生率を低減し、高品質な製品を安定して生産できます。たとえば、カメラレンズの曲率やセンサーの配置精度など、ミクロン単位の精度が求められる工程で有効です。

2. コスト削減

不良品が減ることで、材料やリソースの無駄を削減できます。また、品質検査にかかる時間やコストも抑えることが可能です。Cpk管理により、問題が発生する前に工程のズレを発見できるため、余計な修正作業を減らせます。

3. 顧客満足度の向上

高品質な製品を安定供給できることで、顧客からの信頼が向上します。カメラの性能や耐久性に直結する部品の品質管理にCpkを活用することで、顧客の期待を超える製品を提供することが可能です。

4. リアルタイムでの工程改善

Cpkの監視を続けることで、工程の異常やトレンドを早期に発見できます。例えば、製造中に機械のズレが発生した場合でも、Cpk値の変化で即座に対応が可能です。これにより、製造ライン全体の効率が向上します。

5. 規格外のリスクを可視化

規格外の製品が発生するリスクを事前に可視化し、予防措置を取れるのもCpk管理の大きなメリットです。例えば、センサー感度の測定値が下限規格に近づいている場合、すぐに調整を行い不良品の発生を防ぐことができます。

製造現場でCpk管理を行うことは、品質向上だけでなく、生産効率やコスト削減、顧客満足度の向上に直結する重要な取り組みです。カメラのような精密機器の製造には、特に欠かせない手法と言えるでしょう。

Cpkと不良率の関係をわかりやすく解説

Cpk（工程能力指数）は、製造工程の品質を数値化する指標であり、不良率と密接に関係しています。不良率を正確に予測し、低減するためには、Cpkの値とその意味を理解することが重要です。

1. Cpk値が示す品質の基準

Cpkの値が高いほど、工程が規格範囲内で製品を安定的に生産できていることを意味します。具体的には、以下のような基準で評価されます。

Cpk = 1.0: 規格範囲内に99.73%の製品が含まれる。
Cpk > 1.33: 高い工程能力を示し、不良率が極めて低い。
Cpk < 1.0: 規格範囲外に製品が多く含まれる可能性がある。

例えば、カメラレンズの精密加工においてCpkが1.33以上であれば、不良品がほぼ出ない高品質な状態と言えます。

2. Cpk値と不良率の具体的な関係

Cpk値は統計的に不良率を示す標準偏差をもとに計算されるため、直接的に不良率と関連しています。以下は、一般的なCpk値と不良率の関係です。

Cpk = 1.0: 不良率約0.27%（1,000個中約2～3個の不良品）
Cpk = 1.33: 不良率約0.006%（100,000個中約6個の不良品）
Cpk = 2.0: 不良率0.000003%（1,000,000個中約3個の不良品）

例えば、カメラのセンサー製造工程でCpkが2.0に達している場合、ほぼ完璧な品質が保証されます。

3. Cpkが低い場合に不良率が増加する理由

Cpkが低い場合、工程のばらつきが規格範囲を超える可能性が高くなります。これにより、製品の仕様を満たさない不良品が発生しやすくなります。例えば、Cpkが0.8の状態では、不良率が数％に達する可能性があり、特に精密部品の製造では大きな問題となります。

4. 不良率を減少させるためのCpkの向上策

Cpkを向上させることで、不良率を大幅に低減できます。具体的には、以下の方法があります。

工程のばらつきを抑える: 機械の精度向上や温湿度管理などで変動要因を最小化します。
規格中心への調整: 平均値を規格中心に近づけることで、工程のバランスを最適化します。

例えば、カメラ製造の工程で、定期的な設備の点検や校正を行うことで、ばらつきを抑えCpkを改善することができます。

5. Cpkを活用した不良率のモニタリング

Cpkを用いることで、工程の現在の状態をリアルタイムで監視し、不良率の予測を行うことができます。不良率が増加傾向にある場合、Cpkの低下がその兆候として現れるため、早期対応が可能になります。

Cpkと不良率の関係を正しく理解し、工程の管理に反映させることで、不良品の発生を最小限に抑えることが可能です。特にカメラのような精密機器の製造では、Cpkの管理が品質向上の鍵となります。

Cpk計算式で工程改善を最大化する方法

Cpk（工程能力指数）は、製造工程における品質の安定性と適合性を評価するための基本的かつ重要な指標です。

この指数は、製品が規格範囲内に収まるかを数値化し、製造現場での品質改善や不良率削減に役立ちます。特に、片側規格と両側規格という2つの評価方法があり、それぞれ異なる製造要件に対応しています。

片側規格では特定の方向（上限または下限）のみを評価し、無駄な不良判定を防ぐ効率的な管理が可能です。一方、両側規格は上下限の両方を考慮し、全体的なバランスと適合性を重視した評価を行います。

本記事では、これらの計算式と活用方法を初心者にもわかりやすく解説し、カメラ製造工程の具体例を通じてその実用性を詳しく紹介します。

Cpk計算式の秘密：片側規格と両側規格の違いと活用方法

Cpk（工程能力指数）は、製造工程の品質を評価するための重要な指標です。この指標は、片側規格と両側規格のいずれの場合にも適用可能で、それぞれに対応した計算式があります。ここでは、両者の違いとその具体的な計算方法、活用例について解説します。

片側規格に対応したCpk計算式

片側規格の場合、評価対象は規格範囲の片方（上限または下限）のみとなります。例えば、カメラのセンサー感度が「規定値以上」である必要がある場合、この計算式を使用します。片側規格のCpk計算式は以下の通りです： $$Cpk \frac{\text{USL} – \mu}{3\sigma} \quad \text{または} \quad \frac{\mu – \text{LSL}}{3\sigma}$$

ここで：

USL: 上限規格値
LSL: 下限規格値
μ: 平均値
σ: 標準偏差

片側規格では、不要な範囲の評価を除外するため、工程の品質評価を効率化できます。

活用例
カメラ製造では、センサー感度が一定値以上必要な場合や、明るさが特定の閾値を超えることを求められる場合に利用されます。この計算式を適用することで、不必要な不良判定を防ぎつつ、品質を高めることが可能です。

両側規格に対応したCpk計算式

両側規格の場合、製品が上下限の規格範囲内に適合しているかを評価します。この場合の計算式は以下の通りです：$$ Cpk = \min \left( \frac{\text{USL} – \mu}{3\sigma}, \frac{\mu – \text{LSL}}{3\sigma} \right)$$

この式では、上下限のどちらか一方に偏った場合でも、その偏りを考慮したCpk値が算出されます。

活用例
カメラレンズの直径やセンサーの配置精度の管理において、この計算式が用いられます。上下限の規格が設定されている項目に適用することで、不良品率を低減し、一貫性のある高品質な製品を生み出せます。

片側規格と両側規格の違いと使い分け

項目	片側規格	両側規格
評価範囲	上限または下限の片側のみ	上限と下限の両方を評価
計算式	(USL−μ)/3σ または (μ−LSL)/3σ	min⁡{(USL−μ)/3σ ,(μ−LSL)/3σ)}
適用例	センサー感度、明るさ（規定値以上が必要な場合）	レンズの直径、センサーの配置精度（上下限規格が設定されている場合）
利点	不要な範囲を排除し、効率的に評価可能	両側の偏りを考慮してバランスよく評価可能

片側規格と両側規格のCpk計算式は、それぞれ異なる品質管理のニーズに応えるためのものです。片側規格では不要な範囲を除外して効率的に工程管理が行え、両側規格では全体的なバランスと適合性を評価できます。

カメラ製造のような高精度を求められる分野では、これらの計算式を適切に使い分けることで、品質向上と不良率低減の両立が可能となります。

Excelで手軽にCpkを計算する方法：具体的な手順

Excelを使用することで、Cpkを簡単に計算できます。以下は、初めての方にもわかりやすく順序立てて説明した手順です。

1. データを入力する

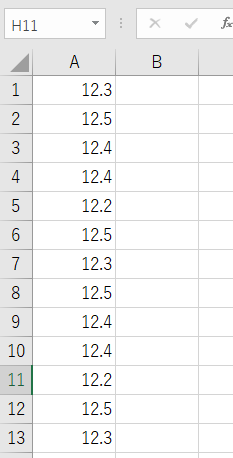
まず、検査結果のデータをExcelシートに入力します。例えば、セル A1～A30 にカメラ部品（レンズの厚みや感度特性）の測定値を入力します。

列 A: 測定データ A1: 12.3 A2: 12.5 A3: 12.4 ... A30: 12.6

2. 規格値（USLとLSL）を入力する

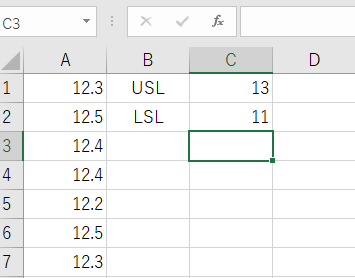
次に、規格の上限（USL）と下限（LSL）をセルに入力します。例えば、セル C1 に USL、C2 に LSL を記入します。

セル C1: 上限規格（USL） C1: 13.0
セル C2: 下限規格（LSL） C2: 11.0

3. 平均値（μ）を計算する

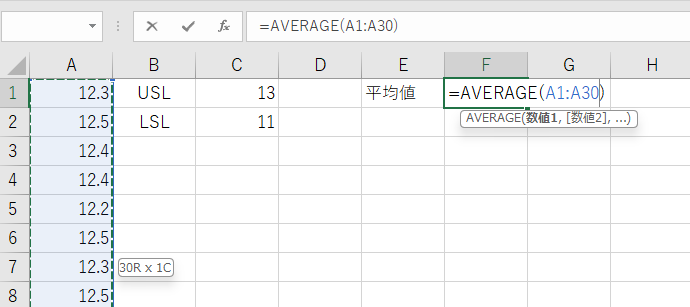
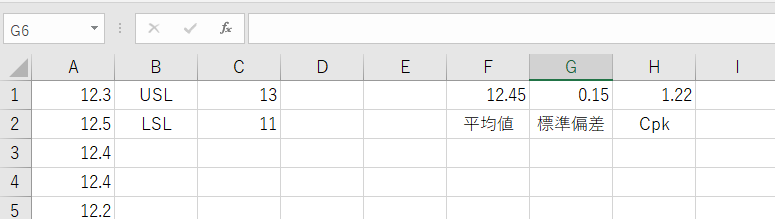
検査データの平均値を求めます。セル F1 に以下の関数を入力してください。

=AVERAGE(A1:A30)

セル F1: 平均値（μ）
例: 平均値が 12.45 となる場合。

4. 標準偏差（σ）を計算する

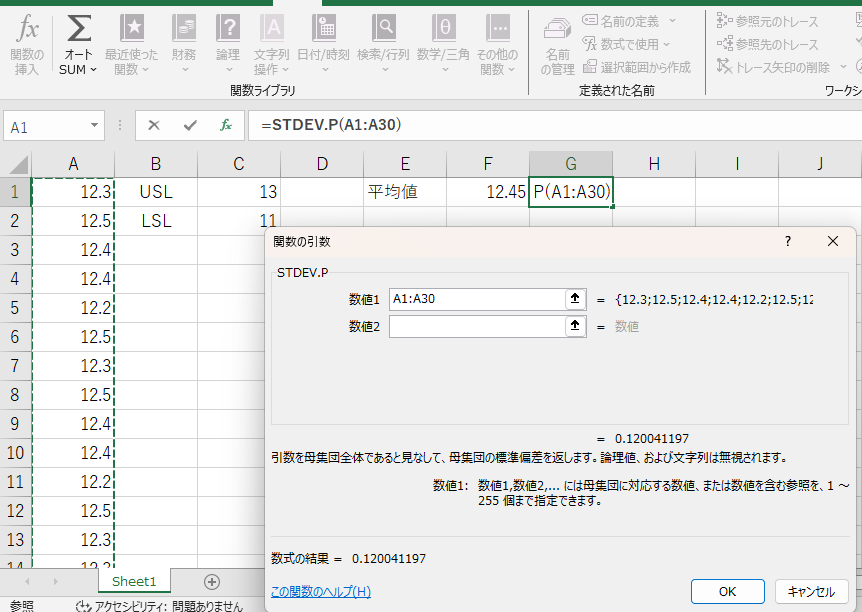
検査データの標準偏差を求めます。セル G1 に以下の関数を入力してください。

=STDEV.P(A1:A30)

セル G1: 標準偏差（σ）
例: 標準偏差が 0.15 となる場合。

5. Cpk値を計算する

Cpk計算式を使ってCpk値を求めます。セル H1 に以下の数式を入力します。

=MIN((C1-F1)/(3*G1), (F1-C2)/(3*G1))

セル H1: Cpk値
例: Cpk値が 1.2 となる場合。

6. 結果を確認する

計算されたCpk値を確認します。この値が 1.33 以上であれば、工程能力が十分であるとされます。

1.33以上: 安定した工程
1.0未満: 改善が必要

●活用例: カメラ部品の品質検査

たとえば、カメラレンズの厚みの測定結果（単位: mm）で、以下の条件があるとします。

上限規格（USL）: 13.0
下限規格（LSL）: 11.0
測定データ: 平均値（12.45）、標準偏差（0.15）

この場合、Cpk値は計算結果で 1.2 となり、工程の改善余地があることがわかります。

●注意点

測定データは最低30点を収集することを推奨します。
STDEV.P（母集団の標準偏差）を使用することに注意してください。
Cpk値が低い場合、不良率が高まる可能性があるため、工程改善を検討しましょう。

この手順を使えば、誰でも簡単にCpk値を算出し、製造工程の品質管理に活用できます。

標準偏差（σ値）がCpkに与える影響とは

標準偏差（σ値）は、Cpk値に直接影響を与える重要な要素です。σ値が小さいほど、製造工程が規格内に集中しやすくなり、Cpk値が高くなります。一方で、σ値が大きいと製品のばらつきが増え、Cpk値が低下します。

例えば、カメラのセンサー感度を管理する場合、測定値のばらつきが大きいと、設定した基準を満たさない製品が増える可能性があります。標準偏差を最小限に抑えるためには、精度の高い機器を使用し、工程の安定性を確保することが重要です。

無料のCpk計算サイトで作業効率をアップ

無料のCpk計算サイトを活用することで、作業効率を大幅に向上させることができます。これらのサイトでは、データを入力するだけでCpk値や関連する指標を自動的に算出できます。

カメラ製造工程では、例えば検査結果をその場で入力し、リアルタイムでCpk値を確認することが可能です。また、これにより、複雑な計算式を手動で解く必要がなくなり、時間を節約できます。ただし、信頼性の高いサイトを選ぶことが重要です。

Keisanサイト様 URL：https://keisan.casio.jp/exec/system/1568794724

swetake.com様 URL：https://www.swetake.com/qc/cpk/onlineCalc/calcCpk.html

Cpkが低い原因と改善策を徹底解説

Cpkが低い場合、それは製造工程において重要な課題を示しています。原因を明確に把握し、適切な改善策を講じることで、品質の向上が可能です。以下に原因と対策を強化して解説します。

Cpkが低い主な原因

工程のばらつきが大きい
- 原因: 製造設備が老朽化している、または作業手順にばらつきがあることが原因となります。例えば、カメラレンズの研磨工程で機械の精度が低下していると、寸法にばらつきが生じます。
- 影響: 不良率の増加や品質の不安定化を招きます。
工程の中心が規格範囲からずれている
- 原因: 設定不一致や測定器のキャリブレーション不良により、工程の平均値（μ）が規格の中央から外れることが原因です。たとえば、センサーの感度設定がずれている場合、設計意図から逸脱します。
- 影響: 中心がずれることで規格範囲内に収まらない製品が増加し、Cpk値が低下します。
測定データのサンプル数が不十分
- 原因: 測定サンプル数が少ない場合、データの信頼性が低下し、正確なCpk値を算出できません。
- 影響: 実際の工程能力が過小評価または過大評価されるリスクがあります。
外部環境の影響
- 原因: 温度や湿度などの環境変化が工程に影響を及ぼすことがあります。例えば、レンズの製造時に湿度が高すぎると、材料の寸法が変化する可能性があります。
- 影響: 環境要因によるばらつきがCpk値の低下を招きます。

Cpkが低い場合の改善策

機械設備のメンテナンスを強化
- 方法: 機械設備の定期的な点検を実施し、老朽化部品の交換やキャリブレーションを行います。
- 例: カメラレンズの加工設備でスピンドルの精度を確認し、必要に応じて調整を行う。
作業手順の標準化と教育
- 方法: 作業手順書を見直し、作業員に対して徹底した教育を行います。
- 例: センサーの配置工程での手順を標準化し、全員が同じプロセスを遵守するようにします。
統計的プロセス制御（SPC）の導入
- 方法: SPCツールを使用し、工程データをリアルタイムで監視します。ばらつきが許容範囲を超えた場合は即座に対応します。
- 例: レンズの厚みデータをモニタリングし、異常値が検出された場合にアラートを設定。
測定器の校正と環境管理
- 方法: 測定器の定期的な校正と、製造環境の温湿度を一定に保つための管理を行います。
- 例: センサーの感度測定器を毎月校正し、精度を保つ。
サンプルデータの増加
- 方法: Cpkを計算するためのサンプル数を増やし、データの信頼性を向上させます。
- 例: 測定サンプルを10個から30個に増やし、統計的な偏りを低減。

改善策の効果

これらの改善策を実施することで、以下のような効果が期待できます：

工程のばらつきが抑えられることで、安定した品質を確保。
工程の中心が規格範囲の中央に近づき、Cpk値が向上。
不良率の低減と製品の信頼性向上。

Cpkを向上させる5つのステップで品質向上

Cpk値を向上させることは、製品の品質を高めるための重要な取り組みです。以下に、具体例や数値を交えながら、効果的な5つのステップを詳しく解説します。

1. 現状を把握する

目的: 現在のCpk値を把握し、問題のある工程を特定します。
具体例: カメラレンズの直径を測定する工程で、Cpk値が0.8と判明した場合、それは製品のばらつきが大きい、または工程の中心が規格からずれていることを示します。
数値例:
- 規格上限（USL）: 10.5 mm
- 規格下限（LSL）: 9.5 mm
- 平均（μ）: 10.2 mm
- 標準偏差（σ）: 0.2 mm
  → Cpk = min{(10.5 – 10.2) / (3 × 0.2), (10.2 – 9.5) / (3 × 0.2)} = 0.5

2. データを収集する

目的: 問題の原因をデータに基づいて分析する。
具体例: レンズの厚みを30個サンプルとして測定し、標準偏差や平均値を算出します。このデータをもとに、ばらつきの発生原因を特定します。
方法:
- 測定値をExcelなどのツールに入力。
- =AVERAGE(データ範囲)で平均を求める。
- =STDEV.P(データ範囲)で標準偏差を計算。
結果: レンズの厚みばらつきが特定の機械で発生していることが判明。

3. 工程の調整を行う

目的: 工程の平均値を規格範囲の中央に近づけ、ばらつきを減らします。
具体例:
- レンズ研磨機のスピンドル速度を調整し、加工精度を向上。
- 規格範囲の中央（10 mm）に平均値を合わせる。
数値改善例:
- 調整後、平均（μ）: 10.0 mm
- 標準偏差（σ）: 0.15 mm
  → Cpk = min{(10.5 – 10.0) / (3 × 0.15), (10.0 – 9.5) / (3 × 0.15)} = 1.11
  → 工程能力が1.0以上となり、安定した品質を確保。

4. 作業員を教育する

目的: 作業者がCpk向上の重要性を理解し、適切な作業を実施する。
具体例:
- 新規作業員に対して、研磨工程での注意点や測定器の正しい使い方を教育。
- Cpk値が低下した場合の対応手順を共有。
効果: 作業ミスによる工程のずれを防ぎ、品質のばらつきを削減。

5. 継続的な監視と改善

目的: 定期的にデータを確認し、問題発生時に迅速に対応する。
具体例:
- 毎週の工程監査で、最新のCpk値を計算。
- リアルタイムモニタリングツールを導入し、異常が発生した際にアラートを設定。
効果: 問題が拡大する前に対策を講じ、不良率を低減。

Cpk向上のまとめ

これらの5つのステップは、特に高精度を求められるカメラ部品の製造現場で効果的です。Cpk値の向上により、製品品質を安定させ、顧客満足度の向上にもつながります。継続的な努力が、高品質な製品供給を可能にします。

CpkとPpkの違いとは？

Cpk（工程能力指数）とPpk（プロセス能力指数）は、製造現場で工程の品質を測定するための重要な指標ですが、目的や計算方法が異なるため、それぞれの違いを理解することが大切です。

1. 過去データと現在データの対象範囲が異なる

Cpkは、工程が安定していると仮定した上で計算されるため、現在進行中の工程の性能を評価するために使われます。一方で、Ppkは過去に生産されたデータを対象に計算され、実際の結果に基づいた評価を行います。

例えば、カメラ製造工程でCpkは現在のセンサー製造ラインの能力を測る指標として使い、Ppkは過去に生産されたセンサーの品質を振り返るための指標となります。

2. 工程の安定性を考慮するかどうか

Cpkは工程が統計的に安定していることを前提として計算します。そのため、工程の安定性が確認されていない場合には、Cpk値は正確な能力を示さない可能性があります。一方で、Ppkは安定性を考慮せず、ばらつきを含めた全体的な能力を評価するため、不安定な工程でも利用可能です。

例えば、新しいカメラのレンズ組み立てラインを立ち上げた際、初期段階ではPpkを用いて全体的な能力を評価し、工程が安定してからCpkを使用するといった活用が考えられます。

3. 計算式の違い

Cpkは、工程の平均値と規格中心値の偏りや標準偏差を考慮して計算されます。一方、Ppkはサンプル全体の標準偏差（総合標準偏差）を使用して計算されます。この違いにより、Cpkは理論的な工程能力を示し、Ppkは実際の生産結果を反映します。

Cpk:$$Cpk = \min \left( \frac{\text{USL} – \mu}{3\sigma}, \frac{\mu – \text{LSL}}{3\sigma} \right)$$
　　　　　　　　　※σは工程内の標準偏差を使用。
Ppk:$$Ppk= \min \left( \frac{\text{USL} – \mu}{3S}, \frac{\mu – \text{LSL}}{3S} \right)$$
　　　　　　　　　※Sは総合標準偏差（サンプル全体の標準偏差）を使用。

具体例:
規格範囲（USL: 10.5 mm, LSL: 9.5 mm）で、サンプル平均（μ: 10 mm）、標準偏差（σ: 0.2 mm、S: 0.25 mm）の場合：

$$Cpk = \min \left( \frac{10.5 – 10}{3 \times 0.2}, \frac{10 – 9.5}{3 \times 0.2} \right) = 0.83$$

$$Ppk = \min \left( \frac{10.5 – 10}{3 \times 0.25}, \frac{10 – 9.5}{3 \times 0.25} \right) = 0.67$$

4. 実務での使い分け

Cpkは工程の現在の能力を測定するため、リアルタイムでの工程改善に役立ちます。一方、Ppkは過去のデータをもとにした総合的な能力評価のため、品質保証や顧客への報告でよく利用されます。

例えば、カメラ製造工程で日々の工程管理にCpkを使用し、四半期ごとや年次の品質レポートにはPpkを使用することで、効率的な管理が可能です。

5. 工程の信頼性向上への活用

CpkとPpkの両方を活用することで、製造工程の信頼性をさらに高めることができます。Cpkで現在の工程能力を把握し、Ppkで過去のデータを振り返ることで、長期的な視点での品質向上が実現します。

CpkとPpkはそれぞれの役割を理解し、適切な場面で使い分けることが重要です。カメラ製造のように高精度が求められる工程では、両指標を併用することで、安定した品質を実現できるでしょう。

比較表

項目	Cpk	Ppk
対象範囲	現在進行中の工程	過去に生産されたデータ
安定性の考慮	統計的に安定している工程が前提	安定性を考慮せず全体を評価
標準偏差	工程内標準偏差（σ）を使用	総合標準偏差（S）を使用
主な用途	現在の工程能力を評価	過去の品質を総合的に評価
利用場面	日々の工程改善	品質保証や顧客向けのレポート作成

CpkとPpkの使い分け

Cpkの利用場面
- 日々の工程管理や改善に適しています。
- 現在の品質状態を即時に把握し、工程の調整や改善に役立てます。
- 例: カメラレンズの研磨工程で、Cpkを用いて中心値を規格範囲の中央に近づけるための調整。
Ppkの利用場面
- 長期的な品質の総合評価や顧客へのレポートに適しています。
- 工程全体のばらつきを含めた実績データを評価します。
- 例: 1年間に生産されたカメラセンサーの品質を振り返り、次年度の改善計画を策定する。