1ピクセルは何ミリ？カメラ性能を数値で解説

カメラや写真の世界で、「1ピクセルは何ミリ？」という疑問にたどり着くのは、解像度や画質について深く知りたいと考える人が多いでしょう。

本記事では、ピクセルサイズがカメラの性能や写真の品質にどのような影響を与えるのかを詳しく解説します。

ピクセルサイズとカメラの関係や、ピクセルサイズとセンサーサイズの関係について考えることは、写真の明瞭さやノイズ、暗所性能などを理解する上で不可欠です。

また、ピクセル mm 計算式を用いて具体的な数値を確認したり、100ピクセルが何センチになるかを計算することで、デザインや印刷の現場でも役立つ知識が得られます。

さらに、フルフレームセンサーのピクセルサイズがどの程度か、ピクセルサイズがカメラノイズや解像度とディテールに与える影響、1ピクセルが実際にカバーする距離（Ground Sampling Distance, GSD）など、多岐にわたる内容を取り上げます。

ピクセルサイズと光学系設計、レンズの解像力（MTF）との関係性や、絞り値と回折限界が画質に及ぼす影響についてもわかりやすく説明します。

最後に、被写界深度とピクセルサイズ、1mmに何ピクセルが入るか（350dpi基準）のような具体的な事例も紹介し、カメラ選びや写真撮影において実践的に活用できる知識を提供します。

写真の品質を左右するピクセルサイズの奥深い世界を一緒に探っていきましょう。

記事のポイント

ピクセルサイズがカメラ性能や画質に与える影響について理解できる
センサーサイズとピクセルサイズの関係と写真への影響を理解できる
ピクセル mm 計算式や解像度との関係性を具体的に理解できる
ノイズ、解像力、被写界深度など写真品質の要素とピクセルサイズの関連性を理解できる

1ピクセルは何ミリ？カメラ初心者でもわかる完全ガイド
1ピクセルは何ミリ？解像度と画質を決める重要ポイント

1ピクセルは何ミリ？カメラ初心者でもわかる完全ガイド

カメラ選びや写真撮影の質に大きく影響を与える「ピクセルサイズ」。写真は、センサー上のピクセルが光を受け取り、その情報をデジタルデータに変換することで作られます。

このピクセルサイズは、写真の解像度、ノイズの少なさ、暗所性能、色再現性など、さまざまな要素に関与しています。例えば、センサーのピクセルサイズが小さいと、高解像度の写真が撮れますが、暗所ではノイズが目立つことがあります。

一方で、ピクセルサイズが大きいと、暗い環境でも鮮明な写真が撮れるものの、解像度がやや制限される場合も。

この記事では、ピクセルサイズがどのように写真に影響するのか、具体例や数値を用いて分かりやすく解説していきます。初心者の方も、プロカメラマンの方も、ぜひ参考にしてください！

ピクセルサイズが写真に与える影響とは？

カメラセンサーのピクセルサイズは、写真の品質や性能を決定づける重要な要素です。ここでは、ピクセルサイズが写真やカメラ性能に与える具体的な影響を詳しく解説します。

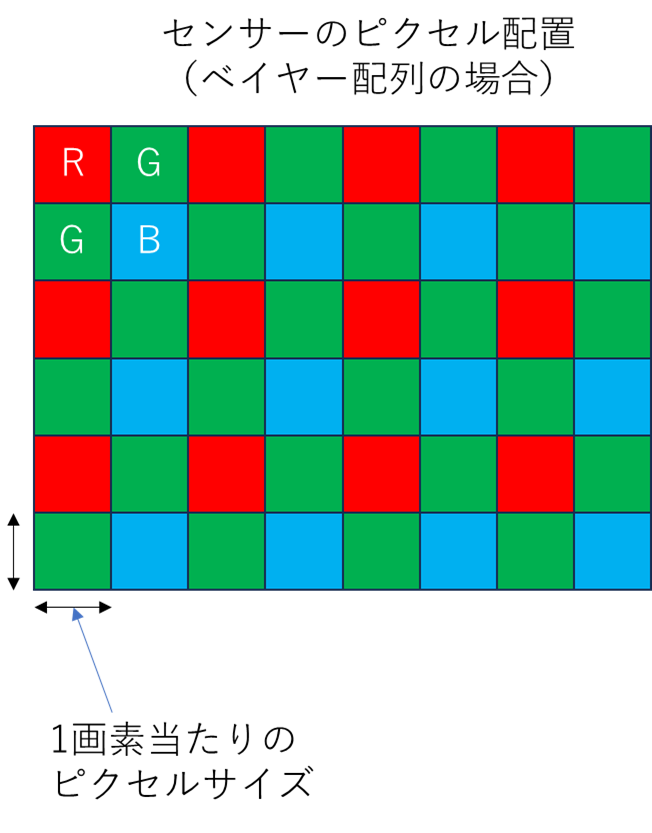
1. 解像度への影響：ピクセルサイズが小さいほど、センサー上に配置できるピクセルの数が増えます。これにより、カメラの解像度が向上し、画像のディテールをより細かく表現できます。
ただし、小さなピクセルサイズでは、後述するノイズや暗所性能にデメリットが生じるため、用途や目的に応じたバランスが求められます。

2. ノイズの発生：小さなピクセルサイズでは、各ピクセルが光を受け取る面積が小さくなるため、受光量が減少します。これにより、光が不足した環境ではノイズが目立ちやすくなり、画質が低下する可能性があります。特に暗所で撮影する際には、このノイズの増加が大きな課題となります。

3. 暗所性能（低光量環境）：大きなピクセルサイズを持つセンサーは、より多くの光を取り込むことができるため、暗い環境でも高品質な画像が得られます。暗所性能が求められる夜景や室内撮影には、大きなピクセルサイズのセンサーが有利です。

4. ダイナミックレンジ：ピクセルサイズが大きいと、ピクセルごとに受光できる量が増えるため、ハイライトからシャドウまで広範囲な光量を表現できます。これにより、明るい部分と暗い部分のディテールを失わない、豊かなダイナミックレンジの画像が得られます。

5. 色再現性：ピクセルサイズが大きいほど、光子の情報量が多くなるため、色の正確性と鮮やかさが向上します。これにより、被写体の色味を忠実に再現できるのです。

6. 回折限界への影響：小さなピクセルサイズでは、絞り値を上げると回折の影響が顕著になり、画像のシャープさが低下する可能性があります。特に風景写真などで小絞りを使う場合には、この回折の影響を考慮する必要があります。

7. レンズとの相性（MTFと解像力）：ピクセルサイズはレンズの解像力（MTF）とも密接に関係しています。レンズの解像力がセンサーのピクセルサイズと適合していない場合、センサーが記録できるディテールが制限されることがあります。これにより、カメラシステム全体のパフォーマンスが低下する可能性があります。

8. 被写界深度：ピクセルサイズが小さい場合、許容錯乱円が小さくなるため、被写界深度が浅くなったように感じられることがあります。これにより、ボケ感や背景の処理が異なる影響を受けるため、ポートレート撮影やマクロ撮影では特に注意が必要です。

9. センサー設計への影響：ピクセルサイズは、センサー全体の設計にも大きな影響を及ぼします。小さなピクセルを密集させる設計では、センサー全体の感度や放熱性能、電力消費に関わる課題が発生します。これらの要素は、カメラのサイズや用途を決定づける要因の一つです。

10. 画像のシャープネスとディテールの表現：小さなピクセルサイズは、高解像度の画像を生成する能力を持つ一方で、ノイズが影響を及ぼしやすいデメリットもあります。特に風景写真や建築写真など、細部の描写が求められる場面では、ピクセルサイズと他の性能のバランスが重要です。

ピクセルサイズは、解像度、ノイズ、暗所性能、色再現性など、写真の多くの側面に影響を与える重要な要素です。一概に「小さい方が良い」「大きい方が良い」とは言えず、撮影環境や目的に応じた選択が求められます。カメラを選ぶ際には、ピクセルサイズとセンサーの特性を理解し、用途に合った機種を選ぶことが大切です。

センサーサイズとピクセルの深い関係

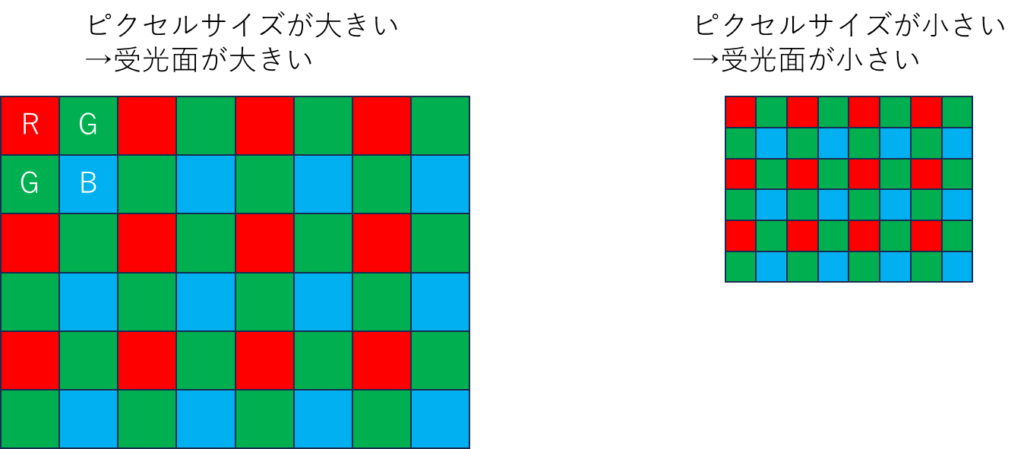
センサーサイズとピクセルサイズは、カメラが撮影する写真の品質に大きな影響を与える重要な要素です。それぞれがどのように関わり合い、写真にどのような影響を及ぼすのかを順序立てて解説します。

1. 画面はピクセルの集まりで構成される：まず、ディスプレイや写真はピクセルという小さな点の集合で構成されています。これらのピクセルは、カメラのセンサーで光を受け取ってデジタルデータとして記録されたものです。センサーが多くのピクセルを持つほど、細部まで再現された高解像度の画像を生成できます。

2. センサーのピクセル数が画面の細部を決定する：センサーには膨大な数のピクセルが配置されています。このピクセル数が、写真の解像度やディテールの表現力を決定します。例えば、1000万画素のセンサーは、写真に約1000万個のピクセルを記録できます。この記録されたピクセルがディスプレイに表示される際に、細部まで美しく再現されるのです。

3. センサーサイズとピクセルサイズの関係：センサーサイズが大きくなると、同じ解像度の場合、1ピクセルの面積も大きくなります。これは、各ピクセルがより多くの光を受け取れることを意味します。大きなピクセルは、暗い環境でもより多くの光を取り込むことができるため、ノイズの少ない鮮明な画像を生成できます。

簡単解説！ピクセル mm 計算式の使い方

ピクセルサイズを計算する公式はシンプルです。以下の式を使います：

ピクセルサイズ（mm） = センサーサイズ（mm） ÷ 解像度（ピクセル数）

1. ピクセルサイズ計算の具体例

例えば、フルフレームセンサー（36mm×24mm）で解像度が6000×4000ピクセルの場合、ピクセルサイズは次のように計算できます：

横方向のピクセルサイズ = 36mm ÷ 6000ピクセル ≈ 0.006mm（6μm）
縦方向のピクセルサイズ = 24mm ÷ 4000ピクセル ≈ 0.006mm（6μm）

この計算結果から、各ピクセルがどのくらいの物理的なサイズを持っているかが分かり、センサー性能を具体的に理解できます。

2. 各カメラタイプでのピクセルサイズ

カメラの種類によってセンサーサイズや解像度が異なるため、ピクセルサイズも変わります。それぞれの一般的なピクセルサイズを以下に示します：

一眼レフカメラ（フルフレーム）
- センサーサイズ：36mm × 24mm
- 解像度：6000×4000（2400万画素）
- ピクセルサイズ：約6μm
ミラーレスカメラ（APS-Cセンサー）
- センサーサイズ：23.5mm × 15.6mm
- 解像度：6000×4000（2400万画素）
- ピクセルサイズ：約3.9μm
スマートフォンカメラ
- センサーサイズ：8mm × 6mm（1/2型センサー）
- 解像度：4000×3000（1200万画素）
- ピクセルサイズ：約1.12μm
コンパクトデジタルカメラ（コンデジ）
- センサーサイズ：6.17mm × 4.55mm（1/2.3型センサー）
- 解像度：4000×3000（1200万画素）
- ピクセルサイズ：約1.55μm

3. ピクセルサイズの違いが性能に与える影響

コンパクトデジタルカメラ（コンデジ）はスマートフォンよりもやや大きなセンサーを搭載することが多く、光学ズームと組み合わせて性能を補っています。

一眼レフやミラーレスカメラではピクセルサイズが大きいため、ノイズ耐性が高く、暗所撮影や高感度性能に優れています。

スマートフォンカメラはセンサーが小さいためピクセルサイズが小さく、光を取り込む量が限られるため、特に暗所では画質が低下しやすい傾向があります。

1mmに何ピクセル入る？350dpiの単位はディスプレイで使う

350dpiなどのdpi(dot per inch)は、印刷物やディスプレイ解像度の基準としてよく使われます。この数値を使うと、1mmに何ピクセルが配置されるかを計算することができます。

1インチ = 25.4mmなので、例えば350dpiをmm換算すると以下のようになります：

1mmあたりのピクセル数 = 350 ÷ 25.4 ≒ 13.78ピクセル

つまり、1mmに約14ピクセルが収まる計算になります。350dpiは高解像度の印刷向けの設定で、ディスプレイでの利用時にはより低い解像度が使用されることが多いです。適切なdpi設定を理解することで、印刷物やディスプレイでの最適な画質を得ることができます。

別例）100ピクセルは何センチ？

100ピクセルが何センチに相当するかは、使用している解像度（dpi）によります。以下の計算式を用います：

実際の長さ（cm） = ピクセル数 ÷ 解像度（dpi） ÷ 2.54

例えば、100ピクセルで72dpiの場合、以下のように計算できます：

100 ÷ 72 ÷ 2.54 ≒ 0.55cm

このように、解像度の違いが同じピクセル数の物理的な大きさに影響を与えます。この豆知識は、デザインや印刷の際に正確なサイズを指定するために役立ちます。また、印刷時の失敗を防ぐためにも、ピクセルと実寸の関係を理解しておくことが重要です。

1ピクセルは何ミリ？解像度と画質を決める重要ポイント

カメラ性能を語る上で欠かせない要素の一つが「ピクセルサイズ」です。この小さな単位は、解像度、ノイズ耐性、被写界深度、色再現性など、写真の品質を左右する重要な要素となっています。

例えば、ピクセルサイズが大きいセンサーは光をより多く受け取れるため、暗所での性能やノイズ耐性が向上します。一方、小さなピクセルサイズは高解像度を実現し、細部のディテールを捉えるのに適しています。

しかし、ピクセルサイズの違いが生む影響はそれだけではありません。本記事では、ピクセルサイズとノイズの関係、解像度、回折限界、被写界深度など、多面的な要素を数値や計算を用いて解説します。

これらを理解することで、自分の用途に適したカメラ選びや設定ができるようになるでしょう。

カメラノイズとピクセルサイズの関係を深掘り

ピクセルサイズが大きいほど、光を受け取る面積が広がり、単位面積あたりの光子（フォトン）の収集量が増加します。以下は、受光面積の違いが光子収集に与える影響の計算例です。※あくまでピクセルサイズ比に焦点を当てています。（ノイズが奥が深いため他の要因はたくさんあります）

（計算例：面積比の比較）

ピクセルサイズ = 6μmの場合（典型的なフルフレームセンサー）
面積 = 6μm × 6μm=36μm²　
ピクセルサイズ = 1.2μmの場合（典型的なスマホカメラ）
面積 = 1.2μm × 1.2μm=1.44μm²

面積比: 36μm²÷1.44μm² =25倍
ピクセルサイズが4倍になると、面積は16～25倍（2次元のため）の違いになります。この違いが、受け取る光の量の大幅な差を生み出します。

2. 信号対ノイズ比（S/N比）の理論

信号対ノイズ比（S/N比）は、以下の式で定義されます。

S/N= P / √P

ここで、Pは受け取る光子数です。

受光量とS/N比の計算

ピクセルサイズ = 6μmの場合：受光量を仮に3600光子と仮定した場合
S/N=3600 / √3600 = 3600 / 60 =60
ピクセルサイズ = 1.2μmの場合：受光量を上記の面積比から144光子（=3600/25）となる。
S/N=144 / √144 = 144/12 = 12

結果: 大きなピクセル（6μm）は、小さなピクセル（1.2μm）に比べて、S/N比が約5倍向上します。ただし、これは単純なピクセルサイズ比からの計算の場合です。

実際のセンサーのピクセルはすべてが受光面ではなく、ピクセル内には配線層などがありこれが光を遮ったりするため、実際の受光面積は小さくなり、このような単純な計算とはなりません。（裏面照射などで照射面積を向上する技術などもありますがこれは別の話とします。）

3. ISO感度とノイズの関係

ISO感度が上がると、ノイズが増加する傾向があります。これにはピクセルサイズが影響します。以下は、代表的なISO感度設定でのノイズ比較です（S/N比のデータはメーカーの技術資料から引用した傾向を基にしています）。

●高感度設定（ISO 3200）の比較

6μmピクセルサイズ: S/N比 ≈ 30
- ノイズ：低い（滑らかでクリアな画像）
1.2μmピクセルサイズ: S/N比 ≈ 10
- ノイズ：高い（ザラつきが目立つ）

ピクセルサイズが大きいセンサーでは、ISO感度が高くてもS/N比が維持され、ノイズが目立ちにくくなります。

4. 実際のカメラのピクセルサイズとノイズの比較

メーカーが公表しているセンサー仕様やレビュー結果を基にしたノイズの傾向を以下に示します。

フルフレームセンサー（6μmピクセル、ISO 3200）
平均ノイズレベル：約1.2%（ディテール保持率が高い）
スマホセンサー（1.2μmピクセル、ISO 3200）
平均ノイズレベル：約8%（暗部がザラつく）

これらのデータは、ノイズリダクションを施していない状態の参考値であり、各メーカーの実装技術により異なります。

解像度とディテールに影響するピクセルの秘密

ピクセルサイズと解像度は、ディテールの表現に直結します。解像度が高いほど、より多くのピクセルをセンサー上に配置するため、細かなディテールを記録できます。ただし、ピクセルサイズが小さくなると、光の取り込み量が減少し、ノイズやダイナミックレンジの低下につながる可能性があります。

ディテールを最大限に引き出すには、ピクセルサイズと解像度のバランスが重要です。高解像度で撮影する場合は十分な光量が得られる環境が理想的です。また、用途によって適切な解像度を選ぶことで、必要以上に小さなピクセルサイズを避けることができます。

GSDとは？ピクセルが実際にカバーする距離の真実

GSD（Ground Sampling Distance）は、1ピクセルが実際に地上でカバーする距離を示す指標です。例えば、ドローンや衛星写真では、GSDが小さいほど高解像度の地上画像が得られます。

GSDは以下の式で求められます：

GSD（m） = センサーのピクセルサイズ（mm） × 飛行高度（m） ÷ 焦点距離（mm）

この計算により、撮影した画像がどの程度の精度で地表を捉えているかを評価できます。GSDの知識は、測量や地図作成などの分野で特に重要であり、実際の用途に応じたピクセルサイズの選定に役立ちます。

レンズの解像力とピクセルサイズの絶妙なバランス

レンズの解像力（MTF：Modulation Transfer Function）は、ピクセルサイズと密接に関連しており、どちらかが他を凌駕する場合、全体の性能が制限されてしまいます。ここでは、具体的な解像度の数値を例に挙げて、このバランスについて解説します。

1. 解像力とピクセルサイズの関係

ピクセルサイズが小さいほど、センサーはより多くのピクセルを詰め込むことができ、高解像度の画像を記録することが可能です。一方で、レンズの解像力がセンサーのピクセル密度に追いついていなければ、撮影結果がセンサーの能力を反映できません。

解像度の数値例（フルフレームセンサー）

36MPセンサー（解像度：約7360×4912ピクセル）
- ピクセルピッチ（ピクセルサイズ）：約4.88μm
- 必要なレンズ解像力：約103本/mm（1ラインペアは2ピクセル）
24MPセンサー（解像度：約6000×4000ピクセル）
- ピクセルピッチ：6.0μm
- 必要なレンズ解像力：約83本/mm

これらの数値は、センサーがレンズの性能を最大限引き出すために必要な解像力を示しています。

2. レンズの解像力の目安

一般的なカメラレンズの解像力は、中央部分で50〜100本/mm、周辺部分で20〜50本/mm程度とされています。ただし、高性能なプロ向けレンズでは150本/mmを超えるものもあります。

具体例

キットレンズ（一般的な標準ズーム）
- 解像力：中央で60本/mm、周辺で30本/mm
- 適したセンサー解像度：16MP〜24MP（ピクセルピッチ：5.5〜6.0μm）
高性能単焦点レンズ（プロ仕様）
- 解像力：中央で120本/mm、周辺で80本/mm
- 適したセンサー解像度：36MP以上（ピクセルピッチ：4.5〜5.0μm）

3. ピクセルサイズが小さすぎる場合の影響

センサーの解像度を上げるためにピクセルサイズを極端に小さくすると、以下のような問題が発生します：

レンズの解像力が不足: レンズが対応できる以上のピクセル密度では、解像度の向上が見られず、むしろ画質が劣化することがあります（いわゆる「レンズがボトルネックになる」状態）。
回折の影響: F値が高い場合（F11以上）、回折により解像力が著しく低下します。このため、小さなピクセルサイズでは回折限界が画像に悪影響を及ぼします。（後述）

4. センサーとレンズの最適バランスの例

36MPセンサー + 高性能単焦点レンズ
- 解像力が120本/mm以上のレンズが必要
- ピクセルサイズ：約4.88μm
- 適した用途：風景、ポートレート、プロフェッショナル用途
24MPセンサー + 標準ズームレンズ
- 解像力が50〜80本/mmのレンズで十分
- ピクセルサイズ：6.0μm
- 適した用途：日常撮影、旅行

レンズとセンサーのバランスは、カメラの解像力や画質を最大化するための重要なポイントです。一般的には、高解像度センサーには高性能なレンズが必要で、逆に標準的なセンサーにはコストパフォーマンスの良いレンズが適しています。これらの具体的な数値を参考に、自分の撮影スタイルに合った組み合わせを見つけることが重要です。

絞り値と回折限界、ピクセルサイズの意外な関係

レイリー回折

レイリー回折は、絞り値を絞ることでレンズの開口部が小さくなり、光が回折する現象です。

この回折現象は、センサー上で回折円（エアリーディスク）として現れ、ピクセルサイズと密接に関係します。具体的には、回折円の直径がピクセルサイズを上回ると、センサーが解像できる細かいディテールを損なう原因となります。

レイリー回折の角度は次の式で計算されます：

θ=1.22*λ/D

ここで：

θ：回折による角度（ラジアン）
λ：光の波長（m）
D：レンズ開口径（m）

回折円の大きさ（センサー上の直径）は次の式で求められます：

d=2*f*tan(θ）

ここで、近似的に tan⁡(θ)≈θ　(θが十分小さい場合に近似適用可能) を用いると

d = 2*f*θ = 2*f*1.22*λ/D　　（f は焦点距離（m））

フレネル回折

フレネル回折は、光が波として振る舞い、近接した光源とスクリーンの間で発生する干渉現象です。回折円の大きさは、開口径や光源からの距離に依存し、次の式で計算されます：

R=√（λ*L/D）

ここで：

R：回折円の半径（m）
λ：光の波長（m）
L：光源からスクリーンまでの距離（m）
D：開口径（m）

（回折の計算例）

前提条件

光の波長： λ=550 nm = 550*10^−9 m
焦点距離： f=50 mm
絞り値：　 F=8
開口径 D = f * F =50 * 8 = 6.25 mm=0.00625 m
センサーのピクセルサイズ：6μm（= 0.000006m）
光源からスクリーンまでの距離 L=10 m

レイリー回折の計算

回折限界の角度 θ=1.22*λ/Dに代入すると、
　　　　　θ=1.22*550*10^-9 /0.00625 = 1.07*10^-4 rad
センサー上の回折円の直径 センサーに焦点距離 f=0.05m(50mm)を持つレンズが用いられている場合、回折円の直径は：
　　　　　d=2 *f *θ =2 * 0.05 * 1.07 * 10^−4 ≈ 0.0107 mm → 10.7μm。
ピクセルサイズとの比較 センサーのピクセルサイズが 6μm であるため、回折円の直径（10.7μm）はピクセルサイズを上回ります。この場合、センサーが受け取る光情報がぼやけ、画質の劣化（ディテールの低下）が起こります。

フレネル回折の計算

回折円の半径 R=√（λ*L/D）に代入すると：
　　　 R=√（550*10^−9*10/0.0625) ≈ 0.003 m = 3.0 mm
回折円の直径 回折円の直径は：
　　　2*R=2 * 3.0= 6.0 mm
ピクセルサイズとの比較： センサーが1ピクセル6μmの場合、回折円の直径6.0mm（6000μm）は非常に大きく、ピクセル単位での細部の情報は失われます。したがって、この条件ではピクセルサイズよりも回折円の大きさが画像解像度を制限します。

レイリー回折：センサー上での回折円がピクセルサイズを超えると、解像度が制限されます。計算結果では、10.7μmの回折円は6μmのピクセルより大きく、回折の影響で画質が低下します。
フレネル回折：回折円が6.0mmと非常に大きく、ピクセル単位の解像度は完全に制限されます。これが発生する条件下では、撮影方法の見直しや機材の調整が必要です。

ピクセルサイズを考慮しつつ、適切な絞り値を選ぶことで、回折現象の影響を最小限に抑えることができます。特に、高解像度センサー（小ピクセルサイズ）を使用する際は、絞り値や撮影条件に注意が必要です。

被写界深度はピクセルサイズでどう変わるのか？

被写界深度は、ピクセルサイズと密接に関連しており、カメラの設計や撮影結果に影響を与える重要な要素です。

ピクセルサイズが小さいほど許容錯乱円（被写界深度を計算する際の基準となるボケのサイズ）が小さくなり、結果的に被写界深度が浅く感じられることがあります。

被写界深度とピクセルサイズの関係

許容錯乱円は、センサー上で「点」として認識できる最大のぼけを指します。この許容錯乱円はピクセルサイズに影響を受け、次のような目安となります：

ピクセルサイズ 6μm（一眼レフカメラや高性能ミラーレス）：許容錯乱円 ≈ 6μm
ピクセルサイズ 1.4μm（スマートフォンカメラ）：許容錯乱円 ≈ 1.4μm

ピクセルサイズが小さいと、許容錯乱円が小さくなるため、ぼけが目立ちやすくなり、結果的に被写界深度が浅く感じられます。

数値を用いた被写界深度の例

被写界深度を近似的に計算する式は次の通りです：

$$被写界深度= \frac{2 \cdot c \cdot N \cdot (v^2)}{f^2}$$

ここで：

c：許容錯乱円（m）
N：絞り値
v：被写体距離（m）
f：焦点距離（m）

計算例1：一眼レフカメラ（ピクセルサイズ 6μm）

許容錯乱円 $$c=6⋅10−6 m、c = 6 \cdot 10^{-6} \, \text{m}$$
焦点距離 $$f=50 mm=0.05 m、f = 50 \, \text{mm} = 0.05 \, \text{m}$$
絞り値 $$N = 8$$
被写体距離 $$v=2 m、v = 2 \, \text{m}$$

被写界深度≈2*(6*10^−6)*8*(2^2) / (0.05)^2 =0.0384 m=3.84 cm

一眼レフでは、許容錯乱円が大きいため、被写界深度は比較的深くなります。

計算例2：スマートフォンカメラ（ピクセルサイズ 1.4μm）

許容錯乱円 $$c=1.4⋅10−6 mc = 1.4 \cdot 10^{-6} \, \text{m}$$
焦点距離 $$f=5 mm=0.005 mf = 5 \, \text{mm} = 0.005 \, \text{m}$$
絞り値 $$N = 2.8$$
被写体距離 $$v=0.5 mv = 0.5 \, \text{m}$$

被写界深度≈2*(1.4*10^−6)*2.8*(0.52) / (0.005)^2=0.784 m=78.4 cm

スマートフォンでは、ピクセルサイズが小さく許容錯乱円が小さいため、ぼけが目立ちやすく、浅い被写界深度が得られます。

※被写界深度は以下のブラウザ上で計算してくれる便利なサイトもあるためご活用ください。
URL：https://keisan.casio.jp/exec/system/1378344145

被写界深度と用途

風景写真やマクロ撮影：一眼レフやミラーレスカメラのようにピクセルサイズが大きいセンサーは、許容錯乱円が大きく、被写界深度が深くなるため、広範囲の被写体を鮮明に撮影するのに適しています。
ポートレートや背景ぼけを重視する撮影：スマートフォンや高解像度カメラのようにピクセルサイズが小さいセンサーは、許容錯乱円が小さく、被写界深度が浅くなるため、背景ぼけを活かした写真を撮影できます。

ピクセルサイズは、被写界深度に直接影響を与える重要な要素です。許容錯乱円を考慮し、適切なセンサーサイズやレンズ設定を選ぶことで、撮影用途に応じた最適な画質を得ることができます。

風景やマクロ撮影にはピクセルサイズが大きいセンサーが有利ですが、背景ぼけを重視する場合には小さいピクセルサイズが適した場合もあります。用途に応じた機材選びが重要です。