統計分析を行う際、データの正確な評価と比較は重要であり、その中でもt検定は広く用いられている手法の一つです。しかし、実際にt検定を実施した後の結果の書き方に悩む人も多いでしょう。本記事では、t検定の基本から検定結果の正しい記述方法までを詳しく解説します。
t検定は、平均値の比較を行う統計的手法であり、カメラ設計や製品開発の評価にも活用されています。特に、標本サイズが小さく母分散が未知の場合に適用されるため、正確な結果を導き出すには適切な手順を理解することが不可欠です。
また、t分布表の読み方やp値の解釈、自由度の計算など、検定のプロセスを適切に記述することが求められます。
本記事では、初心者でも迷わずにt検定の結果をまとめられるよう、具体例を交えながら、レポートや論文に記載する際のポイントを解説します。
t検定の適用範囲やF検定との違い、点推定や区間推定を用いたデータの解釈方法についても詳しく触れますので、統計分析の精度を高めたい方はぜひ参考にしてください。
- t検定の基本概念と結果の適切な書き方
- t分布表や自由度の読み方と活用方法
- p値や有意水準の解釈とレポートへの記載方法
- 点推定と区間推定を用いた統計的なデータの分析方法
初心者でもわかる!t検定 結果 書き方の基本
- 統計上の検定の種類とは
- 検定方法の使い分けについて
- t検定のやり方を解説
- t検定とは?
- t検定の手順
- 例題:カメラ設計におけるレンズ厚みの検定
- t分布表の見方を簡単に理解するコツ
- 母平均 μ に関する点推定と区間推定について
- t分布と正規分布の違いをわかりやすく比較
- 自由度って何?t検定における考え方
統計上の検定の種類とは
統計上の検定には、目的やデータの特性に応じてさまざまな種類があります。
t検定はその中でも「平均値の差を比較するための手法」として広く利用されていますが、その他にも u検定(データが正規分布に従う場合の検定)、χ²検定(カテゴリーデータの関係を検証するため)などがあります。
以下の表では、各検定方法(u検定、t検定、χ²検定、F検定)の特徴と使い分けをわかりやすく整理しました。
| 検定方法 | 特徴 | 使い分け | 具体例 |
|---|---|---|---|
| u検定 | 母分散が既知であり、データが正規分布に従う場合に用いる。 | 平均値の変化を1つの母集団で確認したい場合に使用。 | カメラのISO感度(例:ISO100時のノイズ量)を測定し、基準値からの変化を評価する際に使用。 |
| t検定 | 母分散が未知であり、正規分布に近いデータの平均値を比較する際に使用。 | ・1つの母集団の平均値の変化を確認する場合 ・2つの母集団の平均値を比較する場合に適切。 | カメラAとカメラBのシャープネス値(85と80の平均値)を比較して、有意な差があるかどうかを検証。 |
| χ²(カイ2乗)検定 | カテゴリーデータの分布や、2つのカテゴリの関係を調べる際に使用。 | 質的データ(カテゴリデータ)間の独立性や適合度を検証。 | カメラの色味に対するユーザーの好み(「暖色系が好き」対「寒色系が好き」)を集計し、その好みが異なるかどうかを検証。 |
| F検定 | 2つの母集団の分散の比率を比較する際に用いる。 | 2つの母集団のデータのばらつき(分散)が異なるかどうかを調べる際に使用。 | カメラAとカメラBのシャープネス値のばらつきを比較し、どちらのばらつきが大きいかを検証。 |
検定方法の使い分けについて
u検定のポイント
- データが正規分布に従い、母分散が既知の場合に利用。
- カメラ性能の基準値(例えばISO感度のノイズ基準)からの変化をチェックする場合に便利です。
t検定のポイント
- 2つの母集団の平均値を比較する際に使用。1つの母集団の場合は、平均値の変化を比較
- カメラAとカメラBの測定結果の差を統計的に明確にするのに適しています。
χ²検定のポイント
- 質的データを扱う場合に有効。
- カメラの色味やデザインに関するアンケート結果の集計に用いると、ユーザーの傾向を理解できます。
F検定のポイント
- 分散(ばらつき)の違いを比較。
- シャープネス値や測定結果の一貫性を評価する際に役立ちます。
このように、各検定方法はデータの特性や目的によって適切に使い分ける必要があります。正しい検定方法を選択することで、カメラ性能の比較やデータ解析の信頼性を大幅に向上させることができます。
本記事では、t検定をメインテーマとして具体例を用いて解説します。
t検定のやり方を解説
t検定は統計分析で非常に汎用的な手法であり、大きく分けて2つの場面で利用できます:
- 1つの母集団の変化を確認する場合:例えば、カメラAで撮影した写真のシャープネスが、特定の基準値と異なるかを検証したい場合です。
- 2つの母集団の平均値を比較する場合:例えば、カメラAとカメラBで撮影した写真のシャープネスを比較して、どちらが優れているかを分析したい場合です。
以下では、まず「1つの母集団の変化を検証する場合」について、t分布を解説及び具体例を使って詳しく解説します。
t検定とは?
t検定は、サンプルデータを使って母集団の平均がある特定の値(基準値)と異なるかどうかを判断するための統計的手法です。母分散(ばらつき)が未知の場合に用いられ、t分布という確率分布を利用して解析を行います。
t検定の手順
1. 仮説を設定する
まず、検定の目的に基づいて次の2つの仮説を設定します。
- 帰無仮説(H₀):母平均が基準値と等しい(例:性能が設計基準を満たしている)。
- 対立仮説(H₁):母平均が基準値と異なる(例:性能が設計基準を満たしていない)。
2. 有意水準を設定する
有意水準(α)は、帰無仮説を棄却する基準となる値です。一般的には、α=0.05(5%)やα=0.01(1%)が使われます。本記事ではα = 0.05をメインに解説します。
3. 検定統計量の計算
検定統計量 t0を以下の式で計算します: $$t_0 = \frac{\bar{x} – \mu_0}{\sqrt{\frac{V}{n}}}$$
- xˉ:サンプル平均
- μ0:帰無仮説での母平均(基準値)
- V:サンプルの分散(不偏分散)
- n:サンプル数
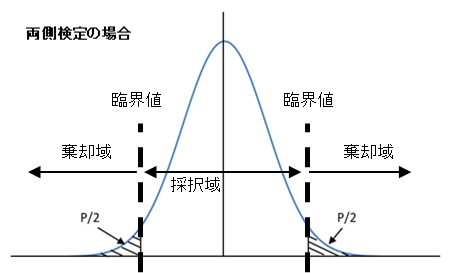
4. 棄却域を決める
棄却域は、有意水準と自由度に基づいて決定します。自由度Φはサンプル数から1を引いた値(n-1)です。t分布表を参照して臨界値(境界値)t(φ, P)を求めます。(t分布表の説明は後述)
5. 検定統計量t0と棄却域を比較する
- 棄却域に入る場合:帰無仮説を棄却(母平均が基準値と異なる)
- 棄却域に入らない場合:帰無仮説を採択(母平均が基準値と等しいとみなす)
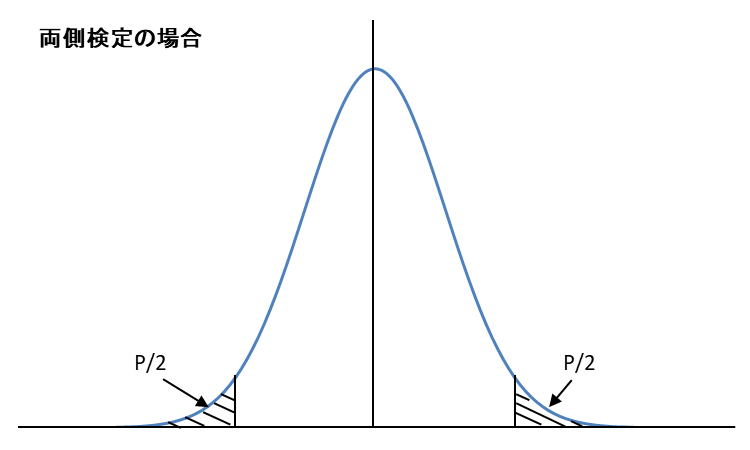
t検定の図のイメージは以下になります。検定推定量t0が、採択域にあるのか棄却域にあるのかを検定します。
例題:カメラ設計におけるレンズ厚みの検定
カメラ設計チームでは、新しいレンズを試作しました。このレンズの厚み(μm単位)の設計基準は20μmであり、±0.5μmの範囲内に収まることが求められています。しかし、試作サンプルから得られたレンズ厚みデータが基準を満たしているかを検定する必要があります。
試作サンプルは以下の通りです: 20.3, 20.5, 19.8, 20.2, 20.4, 20.8, 20.7, 19.7, 19.9
解法
- 仮説の設定
- 帰無仮説(H₀):母平均 μ = 20.0(レンズ厚みは基準値と等しい)
- 対立仮説(H₁):母平均 μ ≠ 20.0(レンズ厚みは基準値と異なる)
- 有意水準の設定
- 有意水準:α = 0.05(両側検定) → 有意水準 α=0.05のt分布表を使う。
- 検定統計量の計算
- サンプルサイズ n = 9
- サンプル平均 $$\bar{x} = \frac{20.3 + 20.5 + 19.8 + 20.2 + 20.4 + 20.8 + 20.7 + 19.7 + 19.9}{9} = 20.37$$
- サンプル分散(不偏分散) $$V = \frac{\sum(x_i – \bar{x})^2}{n-1} = 0.16$$
- 標準誤差 $$SE = \sqrt{\frac{V}{n}} = \sqrt{\frac{0.16}{9}} = 0.133 $$
- 検定統計量:$$t_0 = \frac{\bar{x} – \mu_0}{SE} = \frac{20.37 – 20.0}{0.133} = 2.78$$
- 棄却域の設定
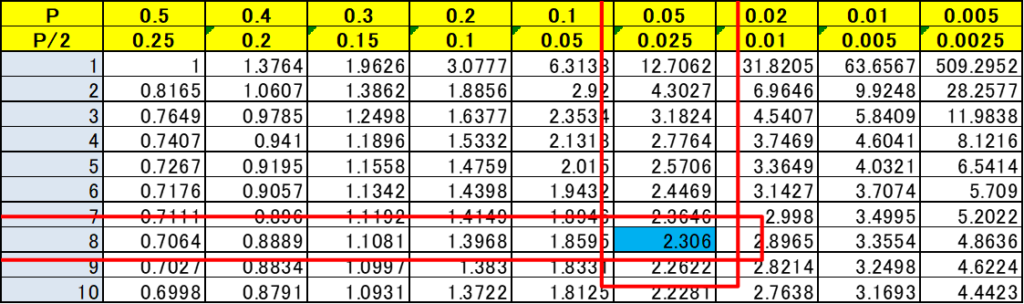
- 自由度 ϕ=n−1=8
- 両側検定で有意水準 α = 0.05 の t分布表(下図)から、臨界値 $$t(8, 0.05) = 2.306$$
- 棄却域:$$|t_0| ≥ 2.306$$
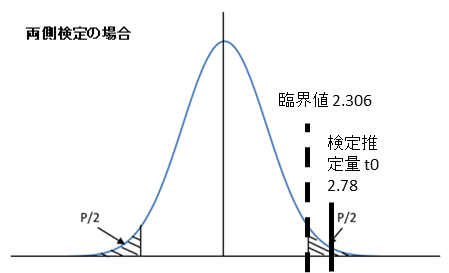
- 判定
- 検定統計量 t0 = 2.78 は棄却域に入る(|2.78| > 2.306)。
- よって、帰無仮説を棄却。(図の斜線が範囲が棄却域)
結論
検定の結果、母平均は設計基準の20μmから有意に異なると判断されました。レンズの厚みは基準範囲内に収まっていない可能性が高いため、設計の見直しや再試作が必要です。
t検定は、データに基づいて母平均が基準値と異なるかどうかを客観的に判断できる強力な手法です。本記事の例題を参考に、カメラ設計やその他の製品設計においてt検定を活用してください。
必要なデータを適切に収集し、正確に計算することで、信頼性の高い結論を導き出せます。
t分布表の見方を簡単に理解するコツ
t分布表は、自由度と確率値(P)の関係を示しています。以下にt分布表の見方やポイントを解説します。
t分布表の構造
t分布表は、自由度Φ(n−1) と 確率P(有意水準 α=0.05など) に基づいて、境界値(臨界値)を示した表です。また、図のイメージは以下となります。
表の読み方
- 行:自由度 ϕ → 標本サイズ n から ϕ=n−1 を計算し、該当する行を探します。
- 列:有意水準(両側または片側) → 両側の確率 P や片側の確率 P/2 に対応するを選びます。
- 交点:臨界値 t (ϕ,α) → 自由度と確率の交差するセルに記載された値が、求める臨界値です。
t分布表の使い方
以下の表が、有意水準α = 0.05の時のt分布表であり、行側が自由度Φ、 列側が確立P(両側P、片側P/2)となります。t分布は正規分布に近い形状をしており、左右対称形状となります。

例題1:片側検定
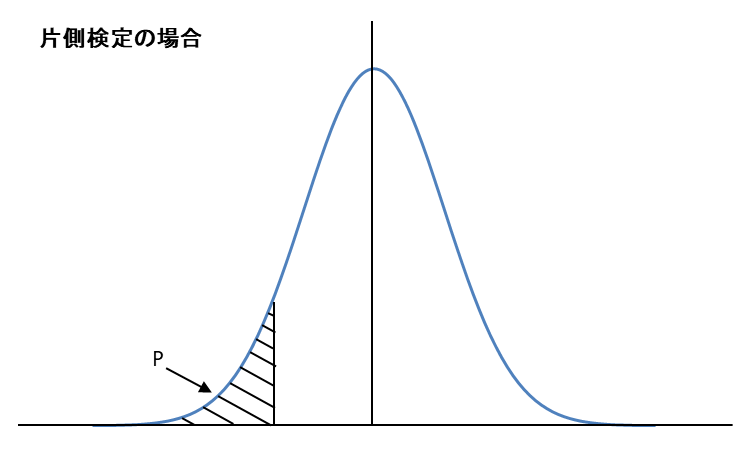
自由度 ϕ=10 の t分布について、「左側の面積が 0.10」となる境界値を求めたい場合:
- 自由度 ϕ=10 の行を確認。
- 両側確率 P=0.20 に該当する列を見る。
- t分布表より: t(10,0.20)=1.372であり境界値は -1.372(左側のため、負の値) です。
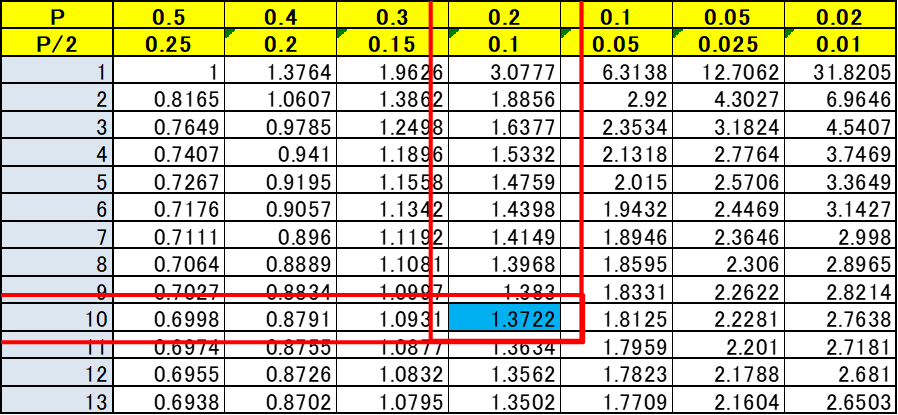
例題2:両側検定
自由度 ϕ=10 で、「両側の合計が 0.05」となる境界値を求めたい場合:
- 自由度 ϕ=10の行を確認。
- 両側確率 P=0.05(片側P/2 = 0.025) に該当する列を見る。
- t分布表より: t(10, 0.05)=2.228であり、左右対称なので、右側の境界値が +2.228、左側の境界値が −2.228 となります。

t分布表とExcelの利用
t分布表を手動で参照することも可能ですが、Excelを使うとさらに便利です。
以下の関数を使うと、簡単に臨界値を求められます:
- 両側検定:
T.INV.2T(P, φ)
例:自由度 10、両側確率 P 0.05 の場合:=T.INV.2T(0.05,10) = 2.228 - 片側検定:
T.INV(P, φ)
例:自由度 10、片側確率 P/2 = 0.1 の場合:=T.INV(0.1,10) = 1.372
ポイント
- 自由度に注意!:自由度 ϕ=n−1を忘れずに計算しましょう。
- 両側と片側の違いを確認!:t分布表は「両側確率」を基準にしていることが多いです。
- 図を描いて確認!:確率がどの部分に対応するか、t分布の図で確認すると間違えにくくなります。
t分布表は、統計学で重要な役割を果たす道具です。特に標本サイズが小さく、母分散が未知の場合に利用されます。
初めて扱うときは少し難しく感じるかもしれませんが、自由度と確率を意識して丁寧に読み取る ことで、正しい値を簡単に求められるようになります。
母平均 μ に関する点推定と区間推定について
1. 点推定
点推定は、母平均 μ の値を1つの数値として推定する手法です。単純に標本平均 xˉをそのまま母平均 μ の推定値として用います。
点推定の式
$$\hat{\mu} = \bar{x}$$
- μ^: 母平均の推定値(ミュー・ハット)
- xˉ: 標本平均
特徴
- 単純で計算が簡単。
- 母平均の推定値を1つの値で表現。
2. 区間推定
区間推定では、母平均 μ が一定の範囲内(信頼区間)に含まれる確率を計算します。母分散が未知の場合には t分布を用いて推定します。
信頼区間の式
$$\bar{x} \pm t(\phi, \alpha/2) \cdot \sqrt{\frac{V}{n}}$$
- xˉ: 標本平均
- t(ϕ,α/2): 自由度 ϕ=n−1 に基づく t分布の臨界値
- V: 標本分散
- n: 標本サイズ
- α: 有意水準(通常 0.05 や 0.01)
信頼区間の解釈
- 信頼率 1−αの場合、母平均 μ がその区間内に含まれる確率は 1−α です。
- 例えば、信頼率95%(α=0.05)では、母平均 μ がその信頼区間に含まれる確率は95%となります。
カメラ設計における推定
カメラレンズの厚みを測定するテストを行った。以下は10個のサンプルデータ(レンズ厚みの値:mm)です:
20.3, 20.5, 19.8, 20.2, 20.4, 20.8, 20.7, 20.7, 19.7, 19.9
- 標本サイズ: n = 10
- 母分散は未知とする。
- 信頼率: 95%(有意水準 α=0.05)。
1. 点推定
標本平均 xˉを計算します: $$\bar{x} = \frac{\sum x_i}{n}$$
$$ = \frac{20.3 + 20.5 + 19.8 + 20.2 + 20.4 + 20.8 + 20.7 + 20.7 + 19.7 + 19.9}{10} = 20.3$$
したがって、点推定値: $$\hat{\mu} = \bar{x} = 20.3$$
2. 区間推定
標本分散 V を計算します: $$V = \frac{\sum (x_i – \bar{x})^2}{n – 1}$$
計算すると: V = 0.1556
次に、標準誤差を求めます: $$\sqrt{\frac{V}{n}} = \sqrt{\frac{0.1556}{10}} = \sqrt{0.01556} \approx 0.1247 $$
t分布の値を参照します: 自由度 10 – 1 = 9、信頼率95%(有意水準 α=0.05)のとき:
$$t(9, 0.05/2) = 2.262$$
信頼区間を計算します: $$\left( \bar{x} – t(\phi, \alpha/2) \cdot \sqrt{\frac{V}{n}}, \bar{x} + t(\phi, \alpha/2) \cdot \sqrt{\frac{V}{n}} \right)$$
$$\left( 20.3 – 2.262 \cdot 0.1247, 20.3 + 2.262 \cdot 0.1247 \right) (20.3−0.282,20.3+0.282)$$
$$\left( 20.3 – 0.282, 20.3 + 0.282 \right) (20.02,20.58)\left( 20.02, 20.58 \right)$$
結果
- 点推定値: μ^= 20.3
- 区間推定値: μ∈(20.02,20.58)
解説ポイント
- 点推定は簡単に計算できますが、信頼区間のように不確実性を考慮しません。
- 区間推定では、信頼率95%の範囲内に母平均があることを示すため、より信頼性のある推定結果を得られます。
- カメラレンズ設計のような精密な分野では、区間推定が有用です。
これにより、設計段階でレンズ厚みの仕様を統計的に評価できます。
t分布と正規分布の違いをわかりやすく比較
統計解析では、データの特性に応じて t分布 と 正規分布 を使い分けます。これらの違いを 「母分散が既知か未知か」 という観点で解説し、最後に比較表で整理します。
- 正規分布: 母分散(ばらつき)が 既知 の場合に使用
- t分布: 母分散(ばらつき)が 未知 の場合に使用
標本データのバラつきを推定する際、母分散がわかっていないときには、代わりに 不偏分散(標本分散) を使用します。この場合、標準正規分布よりも分布の裾が広がるため、t分布 を使用するのが適切です。
分布の形状の違い
- t分布は 標準正規分布と似た形 をしているが、自由度が小さいときに裾が広くなる。
- 自由度が大きくなる(nが増える)と、t分布は 正規分布に近づく。
これは、少ないデータで推定するときの 不確実性を考慮 しているためです。
t分布と正規分布の適用範囲
| 母分散の状態 | 正規分布の適用 | t分布の適用 |
|---|---|---|
| 母分散が既知 | ✅ 使える | ✅ 使える |
| 母分散が未知 | ❌ 使えない | ✅ 使える |
このように、t分布は 母分散の既知・未知にかかわらず使用可能 ですが、母分散が既知の場合は推定精度が高い正規分布を使うのが望ましいです。
正規分布とt分布で信頼区間の幅はどう変わる?
母分散が既知か未知かで、信頼区間の計算結果が変わります。ここで、母分散が既知・未知の両方のケースを比較します。
【例題】
- 標本データ: 21, 20, 23, 20, 20, 19 (n = 6)
- 母分散が 既知: 1.9
- 標本分散: 1.9(不偏分散)
① 正規分布を使った場合
母分散が既知なので、正規分布を使って母平均の 95%信頼区間 を求めます。 $$\bar{x} \pm Z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}}$$
- 平均値 xˉ=20.5
- 標準偏差 σ=√1.9
- 信頼係数(95%)で Z値 = 1.96
- サンプルサイズ n=6
計算: $$20.5 \pm 1.96 \times \frac{\sqrt{1.9}}{\sqrt{6}}$$
結果: $$19.4 \leq \mu \leq 21.6$$
② t分布を使った場合
母分散が未知なので、不偏分散(標本分散)を使い、t分布で 95%信頼区間 を求めます。 $$\bar{x} \pm t_{\alpha/2, df} \times \frac{s}{\sqrt{n}}$$
- t分布表より、自由度5 で t値 = 2.57
- s(不偏標準偏差) = √1.9
- 計算:
$$20.5 \pm 2.57 \times \frac{\sqrt{1.9}}{\sqrt{6}}$$
結果: $$19.1 \leq \mu \leq 21.9$$
正規分布とt分布の信頼区間の違い
| 分布の種類 | 信頼区間の範囲 |
|---|---|
| 正規分布 (母分散既知) | [19.4, 21.6] |
| t分布 (母分散未知) | [19.1, 21.9] |
➡ t分布の方が信頼区間が広い(推定の不確実性が大きいため)。
| 項目 | t分布 | 正規分布 |
|---|---|---|
| 母分散 | 未知のとき使用 | 既知のとき使用 |
| 標本サイズ | 小さいとき(n < 30) | 大きいとき(n ≥ 30) |
| 形状の特徴 | 裾が広い (自由度が小さいほど広がる) | 釣鐘型、裾が狭い |
| 自由度の影響 | 自由度が増えると正規分布に近づく | 自由度の影響なし |
| 推定精度 | 低め(信頼区間が広がる) | 高め(信頼区間が狭い) |
| 適用例 | 小規模データでの平均値比較 | 大規模データでの平均値比較 |
- 母分散が既知なら正規分布を使う(推定精度が高い)。
- 母分散が未知ならt分布を使う(信頼区間が広くなる)。
- t分布は標本サイズが増えると正規分布に近づく。
- データのバラつきを考慮して適切な分布を選ぶことが重要。
このように、t分布と正規分布の違いを理解し、適切な場面で使い分けることで、より信頼性の高い統計解析が可能になります。
自由度って何?t検定における考え方
自由度とは、分析において「サンプルデータが自由に動ける数」を意味します。計算式は、サンプルサイズから制約条件の数を引いたものです。
例えば、カメラAで撮影した写真10枚を比較する場合、自由度は9となります(サンプル数10-1)。自由度が増えるほどt分布は正規分布に近づき、結果の精度が高まります。自由度を理解することで、検定の信頼性を適切に評価できるようになります。
実践で役立つ!t検定 結果 書き方の具体例
- 実践で役立つ!t検定 結果 書き方の具体例
- エクセルで簡単!t検定の結果の書き方
- nsの意味は?t検定 結果 書き方の注意点
- 有意差なしの場合のt検定 結果 書き方
- 対応のないデータを扱うときのt検定 結果 書き方
- t検定とf検定、どちらを使うべき?
- グラフを使ってt検定の結果をわかりやすく伝える方法
- 重要ワードとその解説
エクセルで簡単!t検定の結果の書き方
エクセルを使えば、t検定の計算 を簡単に実施し、結果を整理して分かりやすく記録 することができます。
1. 比較するデータをエクセルに入力
t検定では、2つのデータ群の平均値を比較 して統計的な差があるかどうかを調べます。
今回は、カメラAとカメラBの シャープネス値(lp/mm) を比較する例を使います。
📌 例:カメラAとカメラBのシャープネス値
| カメラA(列A) | カメラB(列B) |
|---|---|
| 85 | 80 |
| 88 | 82 |
| 83 | 79 |
| 86 | 81 |
| 87 | 78 |
2. 関数 T.TEST を使う
エクセルには、t検定を自動計算する T.TEST 関数が用意されています。
この関数を使うことで、t0値(検定推定量)を求められます。
📌 T.TEST関数の書き方
=T.TEST(データ範囲1, データ範囲2, 検定の種類, 両側 or 片側検定)引数の意味
| 引数 | 意味 |
|---|---|
| データ範囲1 | 比較対象の1つ目のデータ(カメラA) |
| データ範囲2 | 比較対象の2つ目のデータ(カメラB) |
| 検定の種類 | 対応なしの場合:2、対応ありの場合:1 |
| 両側・片側検定 | 両側検定:2、片側検定:1 |
実際にエクセルで入力
データがA列(カメラA)、B列(カメラB)に入力されている場合、以下の数式を入力します。
=T.TEST(A2:A6, B2:B6, 2, 2)➡ これは「対応なしのt検定」で両側検定を行う場合の式です。
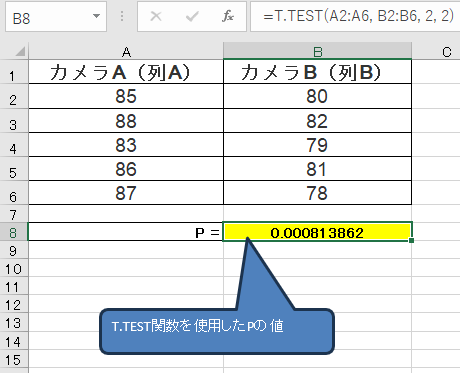
上記の関数でt検定を実行すると、P値が表示されます。
例えば、エクセルで計算した結果が P= 0.0081 となり、次のように解釈します。
| P値 | 判断 |
|---|---|
| t0 < P値(臨界値) | 有意差あり(統計的に差がある) |
| t0 ≥ P値(臨界値) | 有意差なし(統計的な差はない) |
エクセルのT.TEST関数ではt値や自由度が表示されないため、手動で計算する場合は データ分析ツール を利用すると便利です。
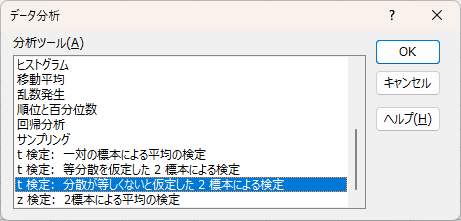
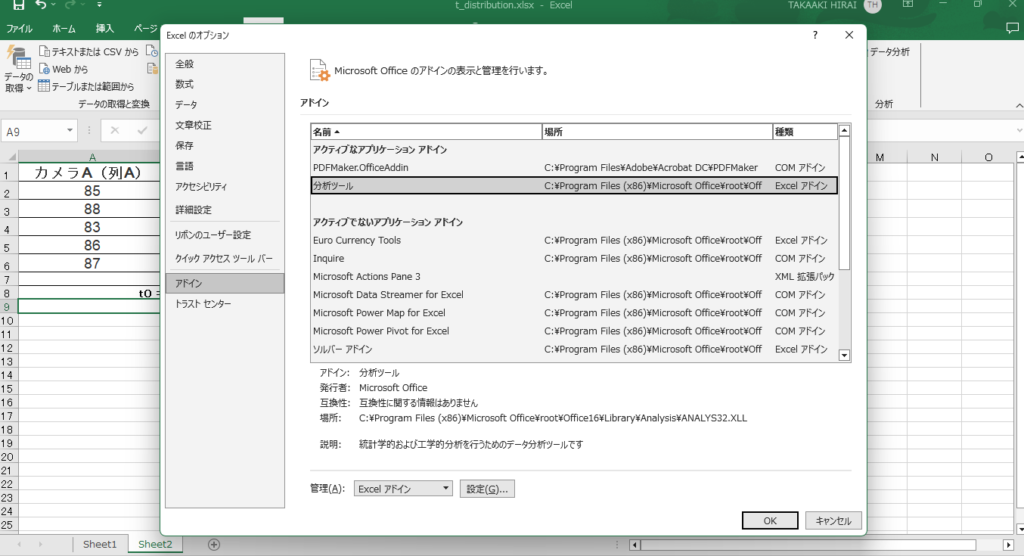
1. エクセルの「データ分析」ツールを使う
① [データ] タブ → [データ分析] をクリック
② 「t検定(分散が等しくないと仮定した2標本による検定)」 を選択
③ [入力範囲] にカメラAとカメラBのデータを指定
④ 出力範囲を設定して「OK」
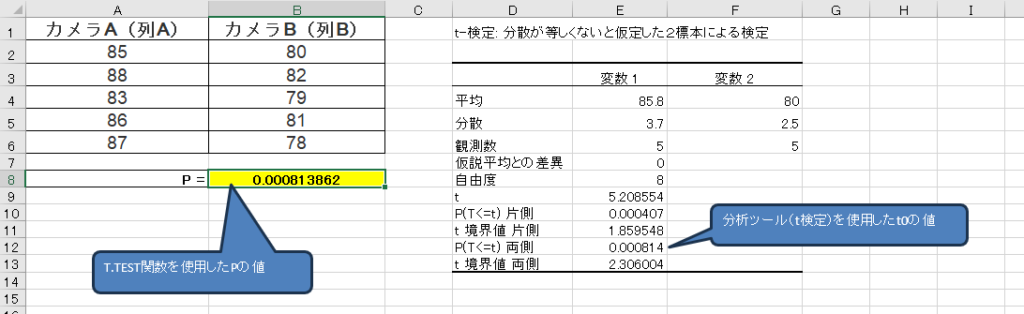
※データタブに、「分析ツール」の表示がない場合、以下の手順を設定する必要があります。
「ファイル」 → 「オプション」 → 「アドイン」を選択し、分析ツールをアドインしてください。
2. 自由度(Φ)の計算
自由度は以下の式で求められます。
Φ = nA + nB – 2 (標本がAとBの2つのため、-2になります。)
📌 例:カメラAとBのサンプル数が5ずつ(nA=5, nB=5)の場合
Φ = 5 + 5 - 2 = 8➡ 自由度は 8 になります。
検定推定量 t0値の計算
t0を算出する関数はエクセルにはないため、データタブの「分析ツール」を用います。
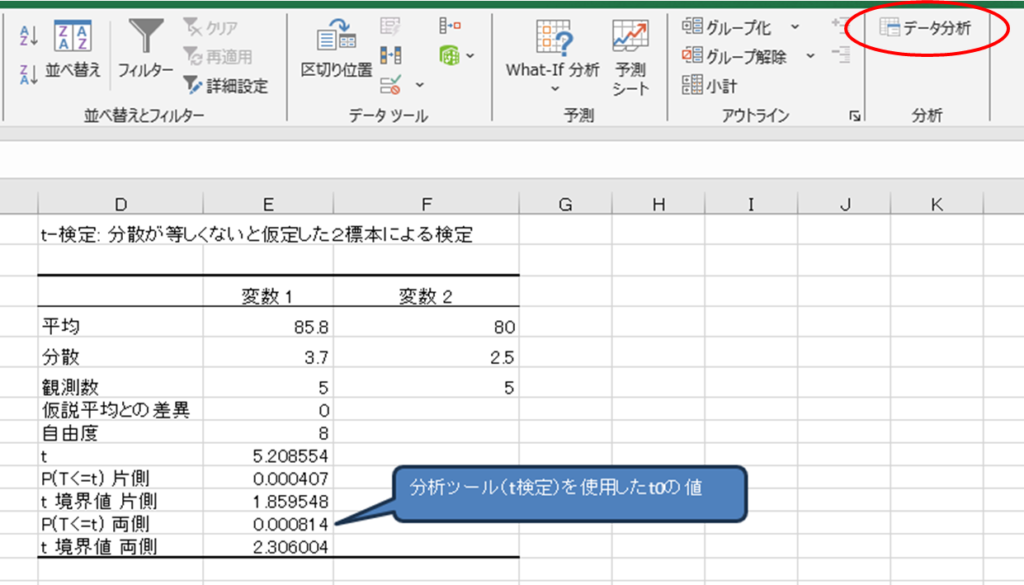
結果を表に整理
計算結果を 表にまとめると見やすくなる ので、次のように整理しましょう。
| 項目 | カメラA | カメラB | 結果 |
|---|---|---|---|
| サンプル数 (n) | 5 | 5 | – |
| 平均値 (x̄) | 85 | 80 | – |
| 分散 | 3.7 | 2.5 | – |
| 自由度 (df) | – | – | 8 |
| t値 (t0) | – | – | 2.306 |
| p値 | – | – | 0.00081 |
| 結論 | – | – | 有意差あり |
📌 この表のポイント
- 数値を簡潔に整理することで 比較しやすくなる。
- 自由度、t値、p値の情報を明記 することで、読者が結果を理解しやすくなる。
✅ エクセルを使ったt検定の手順
- データをエクセルに入力(A列とB列)
- T.TEST関数でp値を算出
- データ分析ツールを使い、t値や自由度を計算
- 結果を表に整理
- レポートとして記載
✅ エクセルでのt検定のポイント
T.TESTを使えば 簡単にp値が算出 できる。- 自由度・t値の計算にはデータ分析ツールが便利。
- 表にまとめて、結果をレポート化すると見やすい。
📌 以上の手順を踏めば、エクセルを活用して 誰でも簡単にt検定の結果を記録 できます!
nsの意味は?t検定 結果 書き方の注意点
t検定の結果で「ns(not significant)」と表示されることがあります。これは「有意差なし」を意味し、データ間に統計的な差がないことを示します。
例えば、カメラAとカメラBでシャープネス値を比較し、p = 0.12の場合、「ns」と判断されます。この場合、以下のように書くことが重要です。
- 「カメラAとBの間に統計的な有意差は認められませんでした(p = 0.12, ns)」
- 注意点として、nsだからといって全く差がないとは限らず、サンプルサイズや測定条件を再確認することが推奨されます。
有意差なしの場合のt検定 結果 書き方
有意差なしの場合、結果を明確に示しつつ、読み手が誤解しないよう工夫が必要です。
例えば、カメラAとBで撮影速度を比較し、p = 0.08で有意差がない場合、次のように記述します。
- 「カメラA(1.2秒)とカメラB(1.3秒)の撮影速度には有意差は認められませんでした(p = 0.08)。」
このとき、「差があるとは限らない」ことを読者に伝えることが重要です。可能であれば、試行回数や測定精度の向上を提案することで、信頼性を向上させる手段を示すと良いでしょう。
対応のないデータを扱うときのt検定 結果 書き方
対応のないデータとは、独立した2つのデータセットを比較する場合を指します。カメラAとカメラBのシャープネス値をそれぞれ別の被写体で測定した場合が例として挙げられます。
以下の手順で記述すると適切です。
- データの性質を明記
「カメラAとBのシャープネス値を、それぞれ独立した被写体で測定しました。」 - 検定結果を具体的に記載
「t検定の結果、p = 0.03であり、カメラAのシャープネスがBに比べて有意に高いことが示されました(t = 2.45, 自由度 = 18)。」
独立したデータの場合、測定条件を詳細に記述することが信頼性の向上につながります。
t検定とf検定、どちらを使うべき?
t検定とf検定は、目的に応じて使い分ける必要があります。
- t検定
平均値の差を比較する際に使用します。例えば、カメラAとBのシャープネス値の平均を比較する場合に適しています。 - f検定
分散の差を検証する際に使用します。例えば、カメラAとBで撮影時の明るさのばらつきが異なるかを比較する場合に有効です。
具体例として、カメラAとBのシャープネスの比較ではt検定(p = 0.01)を使用し、光量の変動を比較する場合にはf検定(p = 0.04)を適用します。このように、目的に応じた選択が重要です。
t検定とF検定を簡潔に比較すると、次のようになります。
| 項目 | t検定 | F検定 |
|---|---|---|
| 目的 | 平均値の差を比較する | 分散(ばらつき)の差を比較する |
| 適用場面 | カメラAとBのシャープネスの平均値を比較 | カメラAとBの光量のばらつきを比較 |
| 計算方法 | 2群の平均値の差 ÷ 標準誤差 | 大きい分散 ÷ 小さい分散 |
| p値の解釈 | p < 0.05 → 有意な平均値の差がある | p < 0.05 → 有意なばらつきの違いがある |
| 具体例 | カメラAとBのシャープネス値の平均を比較 | カメラAとBの光量の変動の大きさを比較 |
- 「平均値を比較」したい → t検定
- 「ばらつきを比較」したい → F検定
例えば、
📷 カメラAとBのシャープネスが違うか? → t検定
📷 カメラAとBの明るさのバラつきが異なるか? → F検定
このように、目的に応じて適切な検定を選ぶことが重要です。
✅ t検定 は「平均値の比較」に使う
✅ F検定 は「ばらつきの比較」に使う
✅ p値 < 0.05 なら有意な差があると判断
✅ 目的に応じてt検定とF検定を使い分けることが重要
📌 統計的な比較をする際は、まず「何を検証したいか?」を明確にしましょう!
グラフを使ってt検定の結果をわかりやすく伝える方法
t検定の結果をグラフで伝えると、読者にとって視覚的に理解しやすくなります。
- 棒グラフを使用
カメラAとBの平均シャープネス値を比較する場合、棒グラフが有効です。誤差範囲を示すエラーバーを追加することで、信頼区間も視覚的に表現できます。 例:
カメラA: 平均85(±5)
カメラB: 平均80(±4) - 散布図を使用
個々のデータポイントを示すことで、分布の違いを伝えられます。たとえば、カメラAとBのシャープネス値を散布図にすると、ばらつきや傾向が直感的に把握できます。 - グラフのキャプションに結果を記載
グラフ下に「カメラAはBに比べて有意にシャープネスが高い(t = 2.45, p = 0.03)」と記載することで、結果を簡潔に伝えられます。
視覚的な要素を活用することで、読者がより深く内容を理解できるようになります。
重要ワードとその解説
●t検定
2つのグループの平均値を比較し、統計的に有意な差があるかを判断する手法。
例)カメラAとBのシャープネス値を比較して、どちらがより鮮明かを検証。
●F検定
2つのグループの分散(ばらつき)を比較し、統計的な違いがあるかを確認する手法。
例)カメラAとBの明るさのばらつきが異なるかを比較。
●χ²(カイ二乗)検定
質的データ(カテゴリデータ)の分布や関係性を調べるための検定。
例)カメラの色味に対する好みの分布を検証。
●u検定
母分散が既知であり、データが正規分布に従う場合に使用する検定。
例)ISO感度のノイズ量が基準値と異なるかを確認。
●点推定
標本から計算される統計量を用いて、母集団の特定の値(例えば平均や分散)を1つの数値で推定する手法。
例)カメラのサンプル撮影で得られた平均シャープネス値を、全てのカメラの平均値として推定。
●区間推定
母集団の真の値が一定の範囲内にある確率を算出する手法。
例)カメラのサンプル撮影の結果から、シャープネスの平均値が95%の確率で[20.02, 20.58]の範囲にあると推定。
●帰無仮説 (H₀)
「差がない」「変化がない」と仮定する仮説。
例)カメラAとカメラBのシャープネス値に違いはない。
●対立仮説 (H₁)
「差がある」「変化がある」と仮定する仮説。
例)カメラAとカメラBのシャープネス値に統計的な差がある。
●有意水準 (α)
帰無仮説を誤って棄却する確率(通常は0.05 = 5%)。
例)p < 0.05 ならば「統計的に有意な差がある」と判断。
●p値(臨界値、境界値)
検定結果が偶然に発生する確率。
例)p = 0.01 ならば、データの差が偶然である確率が1%しかないため、帰無仮説を棄却。
●棄却域と採択域
棄却域:t値が一定の範囲を超えた場合、帰無仮説を棄却する領域。
採択域:t値が棄却域に入らなかった場合、帰無仮説を維持する領域。
●標準誤差 (SE)
標本のばらつきを考慮した標準偏差の推定値。
●検定統計量 (t値, t0)
検定対象の平均値の差を標準誤差で割って算出。
●自由度 (Φ、df)
サンプルデータが自由に変動できる数。(自由度=サンプル数 – 1)
●t分布表
t分布表 は、t検定 の結果を判断する際に使用する表。自由度(Φ)と有意水準(α) に基づき、t値の閾値を確認するためのもの。
●点推定
点推定では、母平均や母分散などの母集団パラメータを1つの数値で推定
●区間推定
区間推定では、母集団パラメータが一定の範囲内にある確率(信頼区間)を算出。これにより、推定結果の信頼性を数値的に表現することが可能。
t検定 結果 書き方の基本とポイント
本記事のまとめを以下に列記します。
- t検定は2つのグループの平均値を比較する統計手法
- 母分散が未知の場合にt分布を利用する
- t検定には片側検定と両側検定がある
- 自由度はサンプル数から制約条件の数を引いて計算する
- 仮説は帰無仮説と対立仮説を設定する
- 検定統計量はサンプル平均と基準値をもとに計算する
- 有意水準は通常0.05や0.01を使用する
- 棄却域はt分布表を用いて設定する
- t値が棄却域に入れば帰無仮説を棄却する
- 信頼区間は母平均が含まれる範囲を推定する
- 点推定は母平均を単一の値で推定する
- ExcelのT.TEST関数でp値を簡単に算出できる
- t検定の結果はt値・自由度・p値を明記する
- 結果をグラフや表で整理すると分かりやすくなる
- 有意差なしの場合も再確認の必要性を記載する








コメント