標準偏差単位の意味とカメラ評価活用法

標準偏差の「単位」について疑問を持つ方は多く、特に品質管理や画像処理の現場では、その理解が製品の信頼性やばらつき評価に直結します。

本記事では、「標準偏差単位」というテーマを中心に、なぜ標準偏差に単位がつくのか、単位がない場合やパーセント表記（相対標準偏差）との違い、また分散との関係などを実例や図解とともに丁寧に解説します。例えば、「標準偏差が10だとどういう意味ですか？」や「標準偏差の単位はなぜルートですか？」といった疑問にも答えながら、1シグマとは何か、ばらつきの目安はどの程度かといった具体的な判断基準も紹介します。

さらに、エクセルでの標準偏差の求め方や計算サイトの活用法も取り上げ、誰でもすぐに使える知識を提供します。品質管理の視点から「標準偏差単位の影響」や「標準偏差単位品質管理」の重要性も取り上げており、分かりやすく実務に落とし込める構成となっています。標準偏差の見方がよく分からない方、例や正規分布との関係を知りたい方にもおすすめの内容です。

記事のポイント

標準偏差に単位が付く理由とその意味
単位のある標準偏差とない場合（RSDなど）の違い
品質管理における標準偏差単位の重要性
分散との違いやルートを取る理由の理解

標準偏差の単位と計算方法を完全攻略
標準偏差の単位とは何か？基本から解説

標準偏差の単位と計算方法を完全攻略

標準偏差は、単なる統計用語ではなく、製品の品質や信頼性、安定性を数値で可視化するための極めて重要な指標です。特にカメラなどの映像機器分野では、露出時間の精度、色温度のばらつき、ISO感度の安定性など、細かな数値の変動が画像品質に直結します。

本記事では、標準偏差の意味や計算方法、読み解き方、そしてそれをどのように評価や製品改善に活用すべきかを、数式・具体例・比較表を交えてわかりやすく解説します。

標準偏差の見方とデータの読み解き方

標準偏差は、単なる数値ではなく「データの信頼性」や「一貫性」を読み解くための重要な統計指標です。平均値が同じでも、標準偏差の大小によってデータの分布特性は大きく異なります。ここでは、データから読み取れる意味をより具体的に理解し、そこから得られる示唆をどのように活用すべきかを詳しく解説します。

標準偏差の読み解きステップ

データのばらつきを的確に評価するためには、以下の4つのステップで標準偏差を読み解くことが重要です。

① 平均値と標準偏差の関係を確認する：まず、標準偏差の数値を見ただけでは判断できないため、必ず平均値との相対的な関係を見る必要があります。
例）平均が100で標準偏差が5なら「全体のばらつきは平均の5%程度」となります。

② データの範囲（分布）を想定する：正規分布が前提であれば、「±1σ」に約68.3%、「±2σ」に約95.4%のデータが収まると予想できます。
例）平均6500K、標準偏差50Kの色温度データなら、およそ6375K～6625Kに約7割のデータが存在していると解釈できます。

③ 許容範囲と比較する：設計仕様や品質基準に対し、データがその範囲内に収まっているかを確認します。
ISO感度の例でいえば、目標値がISO400、許容ばらつき±20であるなら、標準偏差が±10程度ならまず問題ありません。

④ 異常値の検出に活用する：標準偏差が著しく大きい場合は、測定エラーや構造的な問題、製造上の欠陥が潜んでいる可能性があります。逆に、標準偏差がゼロに近い場合も異常（センサーが動作していない、ダミーデータなど）の可能性を示唆します。

読み解き方の具体例

露出時間の安定性：測定値が1/100秒を基準として、標準偏差が±0.005秒である場合、露出制御は非常に安定しており、ブレの少ない撮影結果が期待できます。
センサー出力のバラつき：画像ノイズの強さを100画素単位で測定し、標準偏差が±15画素の場合と±5画素の場合では、後者の方が明らかに安定しており、製品間のばらつきも少ないと判断されます。
ホワイトバランス（色温度）の精度：測定結果：平均6500K、標準偏差100K → 色の再現性が悪く、製品ごとに色調が異なる可能性。測定結果：平均6500K、標準偏差20K → 非常に安定し、色調の一貫性が高いと評価できます。

今後の活用方法：標準偏差からのフィードバック戦略

標準偏差を読み解いた結果を、単なる評価にとどめず、以下のように今後の戦略や改善施策に活用することが重要です。

1. 品質改善のPDCAサイクルに反映：製品ごとの標準偏差を定期的にモニタリングすることで、品質変動の傾向を早期に把握し、設計や製造プロセスの改善点を特定できます。

2. 品質基準の明文化・標準化：特定の項目において「標準偏差は〇以下が理想」といった数値目標を設けることで、社内や取引先との品質基準が明確になり、製造・開発プロセスの標準化が進みます。

3. 新製品のプロトタイピング評価：開発初期段階での評価において、標準偏差の値が小さい＝ばらつきが少ない場合、設計精度が高く、量産においても安定した性能が期待できます。

4. 顧客満足度や市場トラブルの低減：ばらつきの少ない製品は、ユーザーの使用体験の一貫性が向上し、クレームや返品の発生を抑えることができます。これはブランドの信頼にも直結します。

標準偏差は単なる統計用語ではなく、製品性能のばらつきを数値で捉え、改善の方向性を示してくれる強力なツールです。平均値だけでなく標準偏差も並行して分析することで、数値の“裏にある実態”を見抜く力が身につきます。今後は、設計・製造・評価のあらゆる場面でこの指標を活用し、信頼性の高い製品づくりに生かしていくことが求められます。

標準偏差の求め方を4ステップで解説（詳細・数式付き）

標準偏差（Standard Deviation）は、データのばらつきを表す基本的かつ強力な統計指標です。以下の4つのステップを順に行うことで、任意のデータセットに対する標準偏差を求めることができます。

ステップ①：平均値（μ）の算出

まずはデータ全体の平均値（算術平均）を計算します。
数式は以下の通りです： $$\mu = \frac{x_1 + x_2 + \cdots + x_n}{n}$$

例：
イメージセンサーの出力電圧データが次の3つだったとします：
$$\mu = \frac{100 + 102 + 98}{3} = \frac{300}{3} = 100 \, \text{mV}$$

ステップ②：偏差の2乗を求める

次に、各データが平均からどれだけ離れているか（偏差）を計算し、その値を2乗します。$$ (x_i – \mu)^2$$

例：

(100 − 100)² = 0² = 0
(102 − 100)² = 2² = 4
(98 − 100)² = (−2)² = 4

→ 偏差の2乗の合計：0 + 4 + 4 = 8

ステップ③：分散（variance）の算出

偏差の2乗の合計を、データの個数 n で割ると「母分散」、n−1 で割ると「標本分散」となります。実務では標本分散（不偏分散）を使うことが多いです。 $$\sigma^2 = \frac{\sum_{i=1}^n (x_i – \mu)^2}{n – 1}$$

例： $$\sigma^2 = \frac{8}{3 – 1} = \frac{8}{2} = 4 \, (\text{mV}^2)$$

ステップ④：標準偏差（σ）の算出

最後に、分散の平方根を取ることで、標準偏差が求まります。これにより、元データと同じ単位（この場合はmV）になります。 $$\sigma = \sqrt{\sigma^2}$$

例： $$\sigma = \sqrt{4} = 2 \, \text{mV}$$

応用：データのばらつき評価への活用

このようにして求めた標準偏差をもとに、測定データの安定性や品質を数値で判断できます。今回の例では、センサー出力（平均100mV）に対して標準偏差が±2mVであるため、データは比較的一定範囲内に収まっていると評価できます。

たとえば、許容ノイズレベルが±3mVであるとすれば、今回のセンサーは設計仕様を満たしており、製品として問題がないと結論づけられます。一方で、標準偏差が±6mVなど大きくなれば、設計の見直しや製造工程の改善が必要になる可能性もあります。

標準偏差は、平均値だけではわからないデータの“広がり”を見える化する指標です。測定機器や画像センサーなどの評価において、定量的な品質判断ができるため、開発・検査・工程管理すべてにおいて活用価値が非常に高いと言えます。今後の製品評価では、平均値と合わせて必ず標準偏差も確認する習慣を持つことで、より精度の高い分析が可能になります。

分散と標準偏差の違いをわかりやすく比較

分散（Variance）は、データが平均値からどの程度ばらついているかを数値化する統計指標です。計算式は以下の通りです： $$\text{分散} = \frac{1}{n} \sum_{i=1}^{n} (x_i – \mu)^2$$

ここで重要なのが、平均からの差（偏差）を2乗している点です。これはいくつかの理由によります：

正負を打ち消さないため：データ点が平均より大きい場合と小さい場合では、偏差が正と負になります。これを単純に合計して平均してしまうと、全体のばらつきがゼロになることもあります。2乗することで、すべての値が正になり、ばらつきの大きさを適切に反映できます。
外れ値への感度を持たせるため：2乗することで、大きく平均から外れた値の影響が強調されます。これにより、ばらつきの評価において外れ値の重要性を考慮できます。これは製品の品質管理などで、重大なばらつきを見逃さないために有効です。
微分可能な滑らかな関数であるため：数学的な最適化や推定理論においては、2乗誤差（最小二乗法など）が解析的に扱いやすく、理論的にも広く利用されています。

このように、偏差を2乗することは単なる技術的な都合ではなく、ばらつきを正しく、敏感に、理論的に扱うための必然的な手法なのです。

標準偏差とは？なぜ平方根をとるのか

標準偏差（Standard Deviation）は、分散の平方根です： $$\text{標準偏差} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (x_i – \mu)^2}$$

分散が2乗された単位（例：pixel²）を持つため、平方根を取って元のデータと同じ単位に戻す必要があります。これにより、標準偏差はより直感的に理解できる指標になります。

分散と標準偏差の比較表

比較項目	分散（Variance）	標準偏差（Standard Deviation）
定義	偏差の2乗の平均	分散の平方根
数式	$variance$	$stddev$
単位	元の単位の2乗（例：pixel²）	元の単位（例：pixel）
直感性	わかりにくい	わかりやすい
実用場面	理論・解析重視	実務・報告に最適
なぜこうなるか	正負を打ち消さないため2乗する	元の単位に戻すため平方根を取る

評価の具体例で理解する

分散の例：ISO感度の測定値が 390, 400, 410 の場合、平均値は400、偏差は -10, 0, +10。偏差の2乗平均は$$\frac{(-10)^2 + 0^2 + 10^2}{3} = \frac{200}{3} ≈ 66.67 → 分散：66.67（単位：ISO²）$$
標準偏差の例： $$\sqrt{66.67} ≈ 8.16（単位：ISO）$$

→ この「±8.16」のばらつきがユーザーにとって「ISO感度が安定していない」と感じるか、「許容範囲内」と見るかは、仕様や目的によって判断されます。

分散と標準偏差はどちらもデータの変動を測る重要なツールですが、「分散＝理論的分析」、「標準偏差＝実務的解釈」という役割分担があります。分散の2乗には統計的な必然性があり、それを平方根で戻すことで、標準偏差という実用性の高い指標が生まれるのです。カメラ性能のばらつき評価でも、目的に応じて使い分けることが求められます。

標準偏差と正規分布の深い関係を解説

正規分布（Normal Distribution）とは、統計における最も基本的な分布の一つで、平均値を中心として左右対称に広がるベル型の曲線が特徴です。数学的には、次のような確率密度関数で表されます。 $$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(x – \mu)^2}{2\sigma^2} \right)$$

ここで、

μ：平均（データの中心）
σ：標準偏差（ばらつきの大きさ）

正規分布の重要な特性は、データの多くが平均値の近くに集中し、そこから離れるほど頻度が急激に減少することです。これは多くの自然現象や製造データに共通する傾向であり、カメラ機器の品質評価にも応用できます。

正規分布における標準偏差の意味

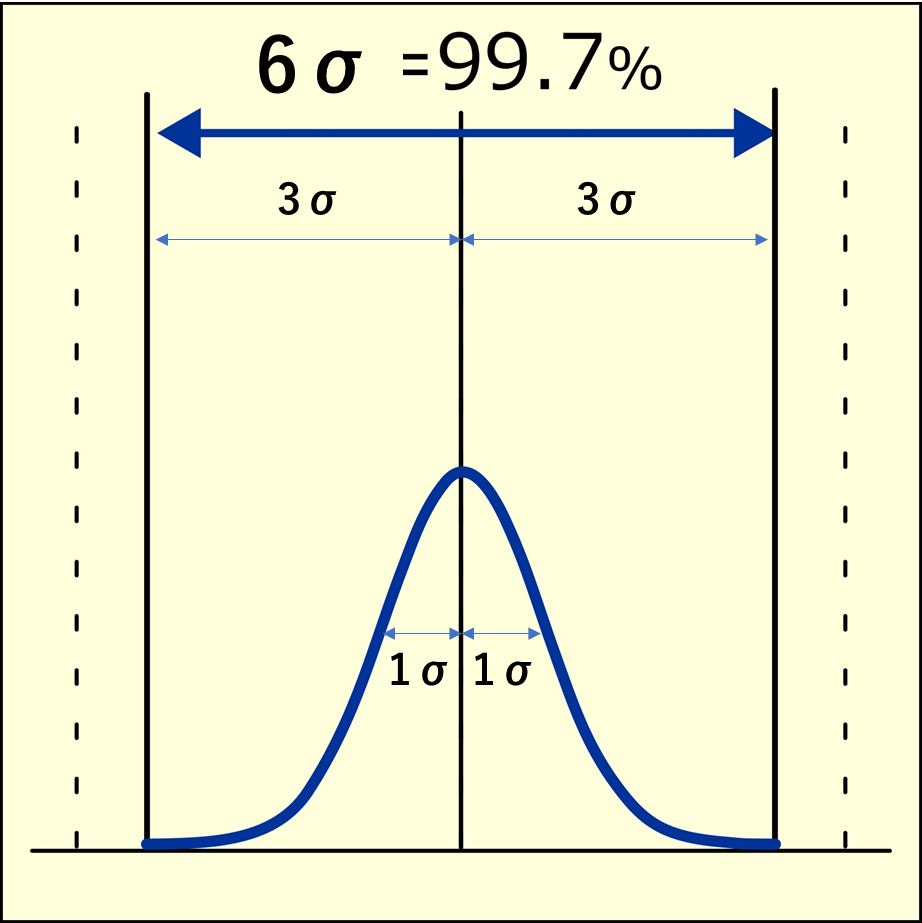
標準偏差（σ）は、正規分布においてデータの広がりを数値的に表す指標です。この広がりは、以下のような確率分布の割合に直結しています：

±1σの範囲（μ ± σ）→ 約68.27%のデータ
±2σの範囲（μ ± 2σ）→ 約95.45%
±3σの範囲（μ ± 3σ）→ 約99.73%

この性質により、製品の測定結果がどの程度安定しているかを定量的に判断できます。

例：シャッタースピードのばらつき

例えば、あるカメラのシャッタースピードの平均が 1/100秒（0.01秒）、標準偏差が 0.001秒 だったとしましょう。
このとき、以下のようにばらつきの範囲が読み取れます：

±1σ → 0.009秒〜0.011秒（約68%のシャッターがこの範囲に）
±2σ → 0.008秒〜0.012秒（約95%）
±3σ → 0.007秒〜0.013秒（ほぼ全数）

このように、標準偏差を使えば「どのくらい製品が安定してシャッターを切れているか」がひと目でわかります。さらに、この分布をグラフ化することで、異常値（例えば0.006秒や0.015秒など）の検出も容易になります。

時系列データと正規分布の応用

時間経過によってばらつきが変動するようなケースでも、正規分布と標準偏差を用いることで定量的な評価が可能です。たとえば、センサーの黒レベル（ダークノイズ）がある日の朝はμ=100、σ=2だったのに対し、午後はσ=5に増加していたとすれば、何らかの環境要因（温度、湿度）や部品劣化が影響している可能性があります。

このような変化を把握することで、予防保全やフィードバック制御への応用も可能となり、製品の信頼性向上に繋がります。

品質管理現場での実践的活用

カメラ製造の現場では、ISO感度、色温度、フォーカス精度など様々な測定値が正規分布を仮定して管理されます。以下のような方法で応用されています：

工程能力分析（Cp, Cpk）に標準偏差を利用し、規格外のリスクを数値化
X̄-R管理図などの統計的品質管理（SQC）ツールで、時間軸での変動を監視
出荷判定時の許容範囲判定に ±2σルールを用いることで、合否を明確化

このように、標準偏差と正規分布を活用すれば、製品が安定して設計通りに動作しているかを統計的に検証できるのです。

Cpkに関する参考記事：Cpk計算式を基礎から解説！工程能力指数の全知識

正規分布は、ランダムなばらつきの背後にあるパターンを示してくれる重要なモデルです。そこに標準偏差を組み合わせることで、データの意味を定量的かつ視覚的に捉えることが可能になります。カメラ性能の分析や品質管理において、この知識は非常に強力な武器になります。

製品の性能や信頼性を語る際、「標準偏差σはいくつか？」「正規分布に従っているか？」という視点を持つことで、経験や感覚ではなくデータに基づいた判断が可能になります。

ばらつきの目安としての標準偏差

カメラの映像品質を定量的に評価する上で、「ばらつき」の把握は欠かせません。標準偏差（σ）は、そのばらつきを数値で示す最も基本的な統計指標であり、製品の一貫性や性能安定性を判断する基準になります。ここでは、実際のカメラ評価項目に即して、標準偏差の目安を具体的に解説します。

1. ホワイトバランス（色温度）の標準偏差

目安：標準偏差 σ ≦ 50K（ケルビン）

ホワイトバランスとは、白色が自然に見えるように色温度を調整する機能です。たとえば、あるカメラ10台の平均色温度が 6500K（標準的な昼光色）だったとし、各台の測定値が以下のようだったとします：

カメラ番号	色温度（K）
1	6480
2	6510
3	6490
4	6520
5	6500
6	6495
7	6505
8	6515
9	6485
10	6500

このときの標準偏差を計算すると約 15.8K となり、十分に安定したカラーバランスといえます。目安としては、標準偏差が50Kを下回っていれば、肉眼での色ズレはほぼ検知されないという研究や業界基準（例：ITU-R BT.709推奨値）に基づいて判断できます。

2. ISO感度のばらつき

目安：標準偏差 σ ≦ 5（ISO値）

ISO感度のばらつきも、画像の明るさとノイズ量に影響を与えるため、重要な評価項目です。たとえば、目標ISO感度が 400 の設定に対し、複数の撮影での実測値が以下のようになっていたとします：

測定回	ISO感度
1	398
2	401
3	397
4	405
5	400

この場合、標準偏差は約 3.1。目標の ±5以内であり、感度制御の安定性が高いと評価できます。業界的には、±5以内であれば露出誤差が±1/6EV以内に収まるため、実用上問題ないとされています。

3. シャープネス（解像力）のばらつき

目安：標準偏差 σ ≦ 10 LW/PH（Line Widths per Picture Height）

シャープネスは、どれだけ細部まで映像を再現できるかの尺度であり、解像性能試験などで測定されます。たとえば、あるカメラの平均解像度が 1000 LW/PH、標準偏差が ±8 LW/PH であれば、約68%のサンプルが992〜1008の範囲に収まると判断できます。このばらつきは画質評価上「高精度」とされ、8K放送機材などの評価基準（例：ARIB TR-B39）でも類似の水準が要求されます。

4. 露出時間の変動（タイミング精度）

目安：標準偏差 σ ≦ 0.01秒

露出時間の標準偏差が大きい場合、撮影画像の明るさに不自然なムラが生じます。たとえば、1/60秒（≒0.0167秒）を指定しているのに、実測値がバラついていると次のようになります：

測定回	露出時間（秒）
1	0.0165
2	0.0167
3	0.0168
4	0.0166
5	0.0169

この場合、標準偏差は約 0.00015秒。極めて高精度であり、露出誤差±1%未満は高性能機の水準です。

標準偏差の目安設定の考え方：標準偏差の目安を定めるには、以下の要素が基準となります：

人間の視覚閾値（色温度差であれば±100K、明るさであれば±0.1EVなど）
業界ガイドライン・国際規格（ISO、ITU、ARIBなど）
製品仕様書に定められた許容範囲
長期信頼性試験による実績値の統計的分析

標準偏差を使うことで、目に見えにくい「ばらつき」が数値で明示されます。カメラのように高精度が要求される機器においては、映像評価項目ごとに適切な標準偏差の目安を設定することで、製品の一貫性を保ち、ユーザーに信頼性のある画質を提供できます。

品質基準に沿った標準偏差の活用は、開発・製造・品質保証のすべての工程で必要不可欠な技術的基盤といえるでしょう。

Excelで標準偏差を計算する方法を完全解説

Excelで標準偏差を計算することは簡単です。以下に具体例をもとに計算する方法を紹介します。

ステップ①：データを入力する

まずは、標準偏差を求めたい数値データをExcelのセルに入力します。
例：カメラのシャッタースピード（単位：秒）を10回測定したデータ

セル	測定値（秒）
A1	0.0165
A2	0.0166
A3	0.0164
A4	0.0165
A5	0.0167
A6	0.0166
A7	0.0165
A8	0.0164
A9	0.0166
A10	0.0165

ステップ②：関数を使って標準偏差を計算する

次に、計算したいセルに以下のように入力します：

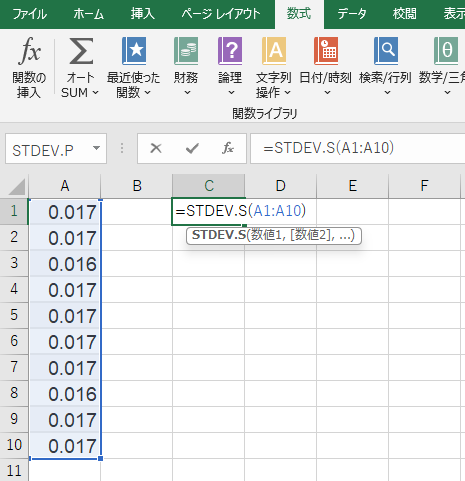
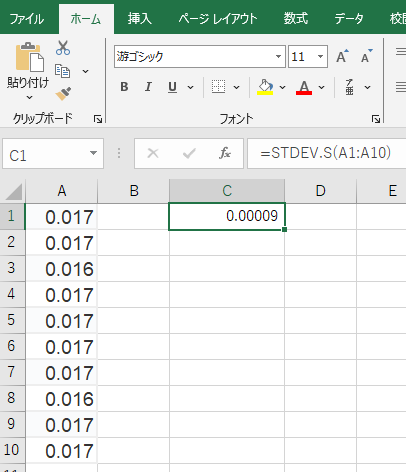
=STDEV.S(A1:A10)
　※値は0.0000948になります。

これで、標本の標準偏差（sample standard deviation） が自動的に算出されます。この結果が例えば 0.0001秒 であれば、「ばらつきが±0.0001秒以内である」と判断できます。

ステップ③：計算結果の確認と分析

計算結果を確認したら、ばらつきの大小を評価します。たとえば、露出時間が毎回0.0165秒前後で安定していれば、シャッター制御の信頼性が高いといえます。さらに、別の機材と結果を比較すれば、どちらのカメラの制御精度が優れているかを判断できます。

ステップ④：グラフで視覚化する（任意）

「挿入」→「グラフ」→「折れ線グラフ」や「散布図」などを使えば、測定値の分布やばらつきを一目で確認できます。ばらつきの傾向が視覚的に分かるため、報告書やプレゼンにも活用できます。

Excelの標準偏差関数の違いと使い分け：Excelでは複数の標準偏差関数が用意されていますが、それぞれ使い分けが重要です。

関数名	意味	使用シーンの例
STDEV.S	標本の標準偏差（sample）	測定値が一部サンプルである場合
STDEV.P	母集団全体の標準偏差（population）	測定値がすべてのデータを含んでいる場合
STDEVA	文字列や論理値を含むデータ用	データにTRUE/FALSEなどが含まれる場合
STDEVPA	母集団で文字列や論理値を含む	母集団全体かつ文字列や論理値を含む場合

選び方のポイント

実験データなど一部しか測れていない場合（多くの実務） → STDEV.S
製品全数の検査結果など完全データの場合 → STDEV.P

Excelを使えば、標準偏差の計算は数式1つで誰でも簡単に実行できます。
特にカメラのような精密機器においては、ばらつきの数値化が品質評価や比較検証の鍵を握ります。関数の違いと使い分けを正しく理解し、統計的な信頼性のある分析を日常業務に活かしましょう。

標準偏差を一発で計算できる便利サイト

最近では、標準偏差を簡単に算出できる無料のWebツールが多数存在しており、特にカメラの性能評価やノイズ解析において非常に重宝されます。以下に、具体的な便利サイトとその特徴をいくつか紹介します。

Keisan（高精度計算サイト）

「高精度計算サイト」では、数値を入力するだけで平均・分散・標準偏差を自動で算出してくれます。母集団・標本のいずれかを選択可能で、入力形式も柔軟に対応しています。複数のカメラセンサー出力の評価時に便利です。

EasyCalculation

「EasyCalculation」は、視覚的に見やすいレイアウトで、標準偏差の計算だけでなくヒストグラムなどの簡易的なグラフ表示も可能です。ISO感度やホワイトバランスのばらつきを確認する際に役立ちます。

Calculator Soup

「Calculator Soup）」は、母集団・標本両方に対応し、データを入力するだけで平均・分散・標準偏差を迅速に表示します。出力結果のコピーペーストも容易で、レポート作成時にも活用しやすいのが特徴です。

Desmos（オンライン統計計算グラフ）

「Desmos」は、インタラクティブなグラフ作成機能が特徴で、入力したデータからリアルタイムで分布グラフを表示できます。ノイズ分布の傾向やセンサー間のばらつきを視覚的に分析したいときに非常に便利です。

これらのツールは、統計に詳しくない方でも手軽に使える設計となっており、カメラ開発や映像品質の評価業務において、作業効率と精度の両立に貢献します。必要な場面でうまく使い分けることで、測定データの理解と品質管理が格段に向上します。

標準偏差の単位とは何か？基本から解説

標準偏差の「単位」は、統計分析や品質管理において見落とされがちですが、実はデータの解釈精度や比較可能性に直結する非常に重要な要素です。特にカメラや映像機器のように、微細なばらつきが画質や性能に影響を与える製品では、標準偏差の持つ単位が測定結果の信頼性や実用性を左右します。

本記事では、「なぜ標準偏差に単位があるのか」「単位が変わるとどう影響するのか」「RSDなど無次元の標準偏差はどのように使うのか」など、カメラ品質評価の現場で役立つ知識を具体例とともにわかりやすく解説します。

標準偏差の単位はなぜルートなのか？

つまり、標準偏差の単位が平方根（ルート）になる根本的な理由は、標準偏差が分散の平方根として定義されているためです。分散とは、各データ点と全体の平均値との差を2乗し、それらを平均した値です。このとき、単位も数値の単位を2乗したものになります。

したがって、もし元のデータが画素数（pixel）であれば、分散の単位は平方画素数（pixel²）になります。ここで平方根を取ることで、単位も元のスケール、すなわちpixelに戻ることになります。

このプロセスによって、標準偏差は元データと同じ単位を持つことが保証され、直感的な理解がしやすくなります。カメラの解像性能やノイズレベルを評価する際に、データのばらつきがpixel単位で示されることで、実際の画質との対応関係を視覚的に把握しやすくなります。

また、単位が一致していることで異なる統計指標や測定値と比較しやすくなり、特に品質管理や映像解析といった分野では、データ解釈の精度を高めるうえで極めて有用です。

単位がつかない標準偏差のパターン

単位がつかない標準偏差は、データが比率やパーセントといった無次元の形で表現されている可能性が高いです。特に相対標準偏差（RSD: Relative Standard Deviation）のように、測定値のばらつきを平均値に対する割合で示す際にこの形式が使われます。これは、複数の測定条件や装置を比較する上で、数値の絶対値に依存しないため非常に便利です。

カメラの品質評価の場面では、以下のような具体例で使用されます：

ISO感度の安定性評価：たとえば、ISO800に設定した状態で10回測定を行い、その出力値のばらつきが平均値に対して±3%であれば、RSDは3%と表示されます。この結果が小さいほど、ISO設定に対するカメラの応答が安定していることを意味します。
SNR（信号対雑音比）の比較：センサーのSNRが平均40dB、標準偏差が0.8dBであれば、RSDは2%。この値を複数のセンサーモデルで比較することで、どのセンサーがより安定した信号出力をしているかが判断できます。
ホワイトバランスの安定性：D65光源下で撮影したときの色温度のばらつきが、平均6500Kに対して±130Kであれば、相対ばらつきは2%。RSDを使えば、光源の違いやモデル間のバランス安定性も比較しやすくなります。

このような形式は、異なる単位系や評価指標が入り混じるカメラ性能試験において、横断的な比較を行うために非常に有効です。一方で、絶対値との混同によって誤解を招くおそれもあるため、RSDの値を見る際には「分母となる平均値が何か」「評価対象は何か」といった文脈の理解が不可欠です。特に設計基準や顧客要求仕様と比較する際には、相対値の裏にある実測データを照らし合わせて、妥当性を検討する姿勢が求められます。

パーセントで表す標準偏差とは？

パーセントで表現される標準偏差は、統計学的には「相対標準偏差（Relative Standard Deviation：RSD）」と呼ばれます。これは、標準偏差（SD）を平均値（Mean）で割った比率に100を掛けてパーセント表記にしたものです。

数式で表すと：
RSD（％）＝（標準偏差 ÷ 平均値）× 100

このように算出されたRSDは、標準偏差を無次元化した指標であり、データのばらつきを「平均値に対する割合」で把握することができます。単位に依存せず比較が可能であるため、異なる機材や測定条件で得られた結果の比較にも向いています。

活用例：カメラや映像関連機器において、RSDは以下のような場面で非常に有用です：

CMOSセンサーのノイズ評価たとえば、あるCMOSセンサーで10回ノイズ出力を測定したところ、平均出力が300mV、標準偏差が6mVだった場合、
　RSD＝(6 ÷ 300) × 100＝2%
　この場合、ノイズばらつきは平均出力に対して2%の範囲に収まっており、センサー出力が安定していると評価できます。
ISO感度の安定性確認：あるISO400設定で10回撮影した際の感度実測値の平均が410、標準偏差が8であれば、
　RSD＝(8 ÷ 410) × 100 ≒ 1.95%
　このように感度の安定性を割合で表現することで、製品間やセンサー間の比較が直感的に行えます。
ホワイトバランス（色温度）評価：色温度が平均6500K、標準偏差が65Kなら、
　RSD＝(65 ÷ 6500) × 100＝1%
　色再現の安定性の比較において、より分かりやすい指標となります。

RSDの利点と注意点：RSDの大きな利点は、異なる単位系や絶対値の異なるデータを「相対的なばらつき」として統一的に評価できることです。これは、異なる撮影条件、異なるモデル、異なるセンサー間での比較が頻繁に行われるカメラ開発や映像品質管理の現場で特に有効です。

ただし、平均値が極端に小さい場合、RSDが異常に大きくなってしまうため、実際のばらつき以上に数値が誇張されるリスクがあります。このため、RSDを使用する際には、データの絶対値や測定背景も併せて確認し、妥当性を検討する必要があります。

このように、RSDはカメラや映像機器の「安定性」や「製品差異」を評価するうえで、非常に強力かつ汎用性の高い指標といえます。

品質管理における標準偏差の単位とは？

品質管理における標準偏差は、「測定対象と同じ単位」で表されることが基本です。これにより、現場での工程評価や改善活動がより直感的かつ実践的に行えます。

具体例：カメラモジュール製造における単位の一致

カメラ製造においては、以下のように各部品や特性に応じて、標準偏差の単位が明確に定まっています。

測定項目	単位	平均値例	標準偏差例
レンズ焦点距離	mm	28.00 mm	±0.05 mm
ISO感度（光感度）	ISO	400	±5
筐体の厚み	μm（ミクロン）	800 μm	±3 μm
輝度（ディスプレイ）	cd/m²	300 cd/m²	±12 cd/m²

このように、標準偏差が物理単位と一致していれば、目視では見えない微細なばらつきでも数値的に把握でき、製品の品質安定性を数値で裏付けることが可能です。

標準偏差の単位と工程能力の関係

標準偏差は、工程能力指数（CpやCpk）と組み合わせて使用されることで、製造プロセスが設計仕様内で安定しているかどうかを判断するための重要指標になります。

Cp = （許容範囲）÷（6 × 標準偏差）
Cpk = 最小 { (上限－平均) ÷ 3σ, (平均－下限) ÷ 3σ }

たとえば：センサーのISO感度が、仕様範囲390〜410（範囲20）で、標準偏差が±5の場合：

Cp = 20 ÷ (6×5) = 0.67 → 工程能力不足（基準Cp=1.33以上）

このように、標準偏差の単位が合っていなければ、CpやCpkの解釈が正確に行えず、誤った工程判断につながるリスクがあります。

単位が重要な理由：わずかな誤差が画質に影響

カメラでは、ほんの数μmのレンズズレや基板の歪みが、焦点ずれ・色収差・ノイズレベル増加といった画質劣化の原因になります。

焦点ズレ → ボケやシャープネス低下
センサー傾き → 色ずれ・ゆがみ
配線の厚みばらつき → 電気ノイズ増加

したがって、ばらつきを正しく定量化し、「何がどれだけズレているのか」を数値で把握するためにも、標準偏差の単位整合性は極めて重要です。

複数単位の比較には「無次元化」も有効

異なる物理量（mm、g、cd/m²など）を同時に比較する必要がある場合は、以下のように標準偏差を「無次元化」する工夫が必要です。

Zスコア：各値から平均を引いて標準偏差で割る（単位なし）
相対標準偏差（RSD）：標準偏差 ÷ 平均 × 100（％表示）

こうした手法を活用すれば、異なる項目同士のばらつき比較や傾向分析が可能になります。

標準偏差の単位は、測定対象の単位と一致することで、品質管理における実用性が高まる。
工程能力指数の計算では、標準偏差の単位が正確であることが前提。
カメラ製品ではμmレベルのばらつきが画質に大きく影響するため、数値による厳密な管理が不可欠。
異なる単位間での比較には、無次元化（ZスコアやRSD）を活用するのが有効。

標準偏差を正しく理解・運用することは、カメラ品質管理の信頼性と効率性を高めるカギとなります。

単位変更が標準偏差に与える影響

物理量の単位を変換すると、それに伴い標準偏差の数値も比例的に変化します。たとえば、ミリメートル（mm）単位で取得したセンサーの厚みデータをセンチメートル（cm）に換算した場合、標準偏差も同様に10で割られることになります。

これは、標準偏差が測定データと同一の物理単位を有する統計量であるためです。特にカメラにおいては、ハウジング構造やレンズマウントの加工精度がしばしばミクロン（μm）単位で厳密に管理されており、こうした単位変換が評価値に与える影響は決して軽視できません。

評価基準が異なる単位系で比較されると、設計許容差との不整合が生じる可能性があるため、解析時には単位整合性に十分な注意が求められます。

標準偏差が10のときの意味とは？

標準偏差が10であるということは、データが平均値から±10の範囲内におおよそ分布していることを意味します。統計学的にこれは「ばらつき（分散）」の大きさを示す定量的な尺度であり、特に正規分布を仮定した場合には、全データの約68.27％がこの範囲内に収まるとされています（1シグマ＝±1σ）。

カメラの解像度評価における具体例

たとえば、あるカメラ用レンズの解像度を10台の製品で測定したとします。得られたデータの平均が1000 LW/PH（Line Width per Picture Height）、標準偏差が10 LW/PHであった場合：

±1σの範囲：990 ～ 1010 LW/PH
この範囲に約68%の製品（＝7台前後）が入っていると期待されます

つまり、解像力のばらつきが±1%以内に収まっていると考えれば、非常に安定した製品群であると評価できます。

ISO感度の例：ばらつきがどれだけ影響するか

別のケースでは、ISO感度の測定において、平均ISOが400、標準偏差が10の場合：

±1σの範囲はISO 390〜410
製造上の仕様で「ISO感度のばらつきは±15以内」が許容範囲であれば、この標準偏差10という数値は十分に良好な水準と判断できます

一方、許容ばらつきが±5程度の厳密な要求であれば、標準偏差10は問題があると見なされる可能性があります。

標準偏差10が許容されるかの判断軸：標準偏差が10であること自体が良い・悪いというよりは、

設計仕様や許容誤差
他モデルとの比較
市場要求スペック

といった文脈によって、その「良し悪し」が変わります。

評価ポイント：

評価対象	平均値	標準偏差（σ）	±1σの範囲	許容誤差	評価
解像度	1000 LW/PH	10	990～1010	±20	○ 安定
ISO感度	400	10	390～410	±5	× やや不安定

標準偏差が10という値は、「平均から±10以内にデータが集中する」ことを示し、正規分布であれば68%以上の信頼性を意味します。
解像度、ISO感度、色温度など、ばらつきが画質に直結する項目の評価において、標準偏差は非常に有用な判断材料です。
評価の際には、単に標準偏差の数値だけを見るのではなく、許容値や製品設計との整合性を踏まえた判断が求められます。

こうした統計的アプローチを用いることで、製品の信頼性・一貫性を定量的に管理し、高品質な映像機器の開発・出荷へとつなげることができます。

1シグマの意味をやさしく解説

1シグマは「1標準偏差」のことを指し、平均値からプラスマイナス1標準偏差の範囲内に、全データの約68.27%が分布していることを意味します。これは統計学の基本であり、正規分布におけるばらつきの基準として広く利用されています。たとえば、カメラのISO感度やダイナミックレンジといった撮影関連の性能指標を複数回測定した際、その測定値が1シグマの範囲内に収まっていれば、そのカメラの性能は安定していると評価できます。

また、1シグマという概念は、画像処理や品質管理の現場でも重要な判断材料として扱われています。たとえば、センサー出力のばらつきが1シグマ以内に収まっているかどうかは、製品の一貫性を示す重要な指標です。統計的品質管理（SQC）では、これを基準として異常値を特定し、工程の異常を早期に発見するためのモニタリング手法にも活用されます。さらに、性能評価レポートや製品仕様書において、±1σの範囲を明示することで、エンドユーザーにも視覚的かつ数値的な信頼性を提供することができます。

品質評価に役立つ「標準偏差単位」の理解まとめ

本記事のまとめを以下に列記します。

標準偏差はデータのばらつきを示す統計指標である
単位は元データと一致し、理解しやすく実務で扱いやすい
分散は単位が2乗されるため標準偏差で平方根を取る
画素（pixel）やISO値など物理量の評価に直接活用できる
単位付き標準偏差は品質管理での許容差判定に直結する
カメラの解像力・露出時間など精密評価に有効である
RSD（相対標準偏差）は単位を持たない無次元指標である
RSDは平均値に対するばらつきを％で表し比較に適する
単位が異なるデータの比較では無次元化が必須となる
CpやCpkの工程能力指数は標準偏差の単位整合性が前提
単位変換に伴い標準偏差の値も比例的に変化する
ExcelではSTDEV.SやSTDEV.Pで簡易的に計算可能である
小さい標準偏差は性能の安定性や信頼性の高さを示す
過度に大きな標準偏差は工程異常や製品不良の兆候となる
適切な単位管理と見方を習得することで品質評価が高度化する